Previsões e possíveis casos de subnotificação do COVID-19 na síndrome respiratória aguda grave (SRAG).

Esse trabalho foi apresentado na disciplina de Estatística aplicada ministrada pelo Prof. Dr. Francisco Cribari Neto. E teve como inspiração, um trabalho feito pelo Prof. Dr. Marcus Alexandre Nunes.

O professor Marcus Nunes tem um blog (https://marcusnunes.me), recomendo fortemente que vocês acessem.

Não deve ser surpresa para ninguém as reportagens sobre prováveis subnotificações a respeito dos casos de COVID-19. A fim de verificar se essas suspeitas são mesmo procedentes, decidi comparar os números de casos de Síndrome Respiratória Aguda Grave (SRAG) registrados no Brasil e em Pernambuco nos últimos 10 anos, a fim de tentar detectar se houve um aumento nos casos em 2020/2021.

Com a análise inicial, já foi possível ver tanto no Brasil como em Pernambuco um aumento extraordinário no ano de 2020/2021. Foi feito também uma análise sobre a média de casos em relação ao ano de 2020, vendo assim um valor alarmante do ano de 2020. Assim, temos altos indícios de que existe subnotificação do COVID-19.

Fizemos dois métodos de previsão, o primeiro usando o algoritmo de Holt-Winters e o segundo usando o modelo ARIMA. Fizemos uma previsão para as próximas seis semanas e comparamos com o valor real. Tivemos um erro menor no modelo ARIMA, indicando assim como um modelo mais preciso para a série SRAG.

Introdução

Não deve ser surpresa para ninguém as reportagens sobre prováveis subnotificações a respeito dos casos de COVID-19. A fim de verificar se essas suspeitas são mesmo procedentes, decidi comparar os números de casos de Síndrome Respiratória Aguda Grave (SRAG) registrados no Brasil e em Pernambuco nos últimos 10 anos, a fim de tentar detectar se houve um aumento nos casos em 2020/2021.

Como sabemos, infelizmente, não há testes de COVID-19 para todos os suspeitos. A Síndrome Respiratória Aguda Grave (SRAG) possui sintomas muito parecidos com aqueles do COVID-19. Com isso, acredito que, com o avanço da pandemia, é importante que a população tenha noção da quantidade de casos da doença que estão por aí.

Temos um bom acesso a casos registrados de SRAG no site da Fiocruz. Eles desenvolveram uma excelente ferramenta de divulgação chamada , no qual obtive os dados aqui divulgados.

Com isso, faremos uma análise para a série temporal, para tentar identificar se os modelos usuais servem para prever se a um aumento ou decrescimento nos futuros casos registrados de SRAG.

Revisão da Literatura

SRAG

Segundo o , existe duas variações, sendo elas:

• Síndrome Gripal (SG): Indivíduo com quadro respiratório agudo, caracterizado por pelo menos dois (2) dos seguintes sinais e sintomas: febre (mesmo que referida), calafrios, dor de garganta, dor de cabeça, tosse, coriza, distúrbios olfativos ou distúrbios gustativos.

• Síndrome Respiratória Aguda Grave (SRAG): Indivíduo com SG que apresente: dispneia/desconforto respiratório ou pressão persistente no tórax ou saturação de O2 menor que 95% em ar ambiente ou coloração azulada dos lábios ou rosto.

Em casos de COVID-19, existem três critérios parar confirmar a doença:

• Por Critério Clínico: Caso de SG ou SRAG com confirmação clínica associado a anosmia (disfunção olfativa) ou ageusia (disfunção gustatória) aguda sem outra causa pregressa.

• Por Critério Clínico-Epidemiológico: Caso de SG ou SRAG com histórico de contato próximo ou domiciliar, nos 14 dias anteriores ao aparecimento dos sinais e sintomas com caso confirmado para COVID-19.

• Por Critério Clínico-Imagem: Caso de SG ou SRAG ou óbito por SRAG que não foi possível confirmar por critério laboratorial e que apresente algumas alterações tomografias.

Com essas informações, fica claro que pode haver casos de subnotificações do COVID-19 nos dados do SRAG.

Holt-Winters

O método de alisamento exponencial Holt-Winters, ou simplesmente algoritmo Holt-Winters, compreende a equação de previsão e três equações de suavização

• Uma para o nível $l_t$,

• Uma para a tendência $b_t$,

• E uma para a componente sazonal $s_t$.

com os parâmetros de suavização $\alpha$, $\beta$ e $\gamma$ .

Existem duas variações desse método que diferem na natureza do componente sazonal. O método aditivo é preferido quando as variações sazonais são aproximadamente constantes ao longo da série, enquanto o método multiplicativo é preferido quando as variações sazonais estão mudando proporcionalmente ao nível da série. Com o método aditivo, a componente sazonal é expressa em termos absolutos na escala das séries observadas e na equação de nível a série é ajustada sazonalmente subtraindo a componente sazonal. Dentro de cada ano, o componente sazonal somará aproximadamente zero. Com o método multiplicativo, a componente sazonal é expressa em termos relativos (percentagens) e a série é ajustada sazonalmente pela divisão pela componente sazonal.

As Equações abaixo correspondem aos métodos aditivo e multiplicativo respectivamente:

Aditivo

$$\text{Equação de Nivel: }\hspace{0.5cm} l_t = \alpha(y_t -s_{t-m}) + (1-\alpha) (l_{t-1} + b_{t-1})$$ $$\text{Equação de Tendência: }\hspace{0.5cm} b_t = \beta^* (l_t - l_{t-1}) + (1-\beta^*)b_{t-1}$$ $$\text{Equação de Sazonalidade: }\hspace{0.5cm} s_t = \gamma (y_t - l_{t-1}-b_{t-1}) + (1-\gamma)s_{t-m}$$

Multiplicativo

$$\text{Equação de Nivel: } \hspace{0.5cm}l_t = \alpha(\frac{y_t}{s_{t-m}} ) + (1-\alpha) (l_{t-1} + b_{t-1})$$ $$\text{Equação de Tendência: }\hspace{0.5cm} b_t = \beta^* (l_t - l_{t-1}) + (1-\beta^*)b_{t-1}$$ $$\text{Equação de Sazonalidade: }\hspace{0.5cm} s_t = \gamma (\frac{y_t}{l_{t-1}-b_{t-1}} ) + (1-\gamma)s_{t-m}$$

A equação de previsão é dado por $$ \text{Equação de previsão:} \hspace{0.5cm} \hat{y}_{t+h|t} = l_t +hb_t + s_w$$ em que $w=t+h-m(k+1)$

ARIMA

Os modelos ARIMA fornecem outra abordagem para a previsão de séries temporais. A suavização exponencial e os modelos ARIMA são as duas abordagens mais amplamente utilizadas para a previsão de séries temporais e fornecem abordagens complementares para o problema. Enquanto os modelos de suavização exponencial são baseados em uma descrição da tendência e sazonalidade dos dados, os modelos ARIMA visam descrever as autocorrelações nos dados.

Em um modelo de regressão múltipla, prevemos a variável de interesse usando uma combinação linear de preditores. Em um modelo de autorregressão, prevemos a variável de interesse usando uma combinação linear de valores anteriores da variável. O termo autorregressão indica que é uma regressão da variável contra si mesma.

Define-se um modelo autorregressivo de ordem $p$, $AR(p)$, como:

$$ y_t = c+\phi_1 y_{t-1} + \phi_2 y_{t-2} + \cdots + \phi_p y_{t-p} + \varepsilon_t$$

em que $\varepsilon_t$ é um ruído branco com distribuição $N(0,\sigma^2)$. Isso é como uma regressão múltipla, mas com valores defasados de $y_t$ como preditores.

Também é possível em vez de usar valores anteriores da variável de previsão em uma regressão, usar um modelo de média móvel para os erros de previsão. Chamamos esse método como modelo de médias móveis, dado pela equação:

$$y_t = c+\varepsilon_t + \theta_1 y_{t-1} +\theta_2 \varepsilon_{t-2} + \cdots + \theta_p \varepsilon_{t-p}, $$

onde $\varepsilon_t$ é um ruído branco. Referimos a isso como um modelo de média móvel de ordem $q$, $MA(q)$.

Se combinarmos com autorregressão e um modelo de média móvel, obtemos um modelo ARMA. O modelo ARMA, pode ser estendido para o modelo ARIMA, em que ARIMA é um acrônimo para AutoRegressive Integrated Moving Average (neste contexto, “integração” é o reverso de diferenciação).

O modelo ARIMA$(p, q, d)$, tem as seguintes nomenclaturas:

$$ p= \text{Ordem da parte autoregressiva}$$ $$d= \text{Números de diferenças feitas}$$ $$q= \text{Ordem da parte de médias móveis}$$

Percebe-se que,

• Se $p\neq0$ e $q=0$, temos um modelo $AR(p)$,

• Se $q\neq0$ e $p=0$, temos um modelo $MA(q)$,

• A ordem $d$, depende se a série for estacionária ou não.

Aplicação

Os dados analisados foram coletados pelo . Os dados são semanais, do ano de 2011 até 2021. Faremos uma análise descritiva, e em seguida ajustaremos os métodos de previsão de séries temporais usuais e os compararemos.

Para visualizar e comparar um potencial modelo, separamos os dados em treinamento e teste. O treinamento são dados da primeira semana de 2011 até a quadragésima nona a semana do ano de 2020. Os modelos serão construídos com base nos dados de treinamento.

A base de testes é da quadragésima nona semana de 2020 até a terceira semana de 2021. A mesma serve para comparar o valor verdadeiro com o valor predito.

Lembrando que analisaremos duas séries temporais, a série SRAG do Brasil e a série SRAG do estado de Pernambuco.

Análise Descritiva

Podemos ver pelas Tabelas (1) e (2) algumas estatísticas sobre as séries temporais. Na Tabela (1) podemos ver que o valor mínimo de casos ocorridos em uma semana no Brasil foi $14$, e que como a média se difere bastante da mediana e o terceiro quartil, observando então, um grande aumento no número de casos nas semanas finais dos dados. O valor máximo de casos em uma semana foi de $17943$.

Tabela 1 - Algumas Estatísticas para a série SRAG Brasil.

Na Tabela (2) podemos ver também que como a média se difere bastante da mediana e do terceiro quartil, tendo novamente, um grande aumento no número de casos nas ultimas semanas. O valor máximo de casos em uma semana foi de $1312$.

Tabela 2 - Algumas Estatísticas para a série SRAG Pernambuco.

A partir dessa primeira análise, foi feito um gráfico mostrando o número de casos ao longo das semanas, filtrados pelos anos. Com isso, podemos ver os primeiros indícios de subnotificação do COVID-19.

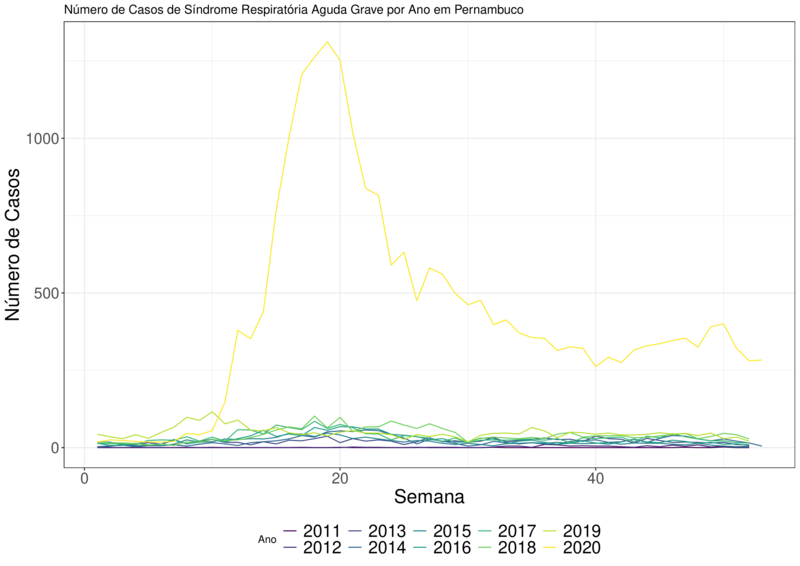
Tanto na Figura (1) envolvendo todo o Brasil, como na Figura (2) envolvendo todo o estado de Pernambuco, o ano de 2020 está claramente destacado por conter uma curva muito superior a todos os outros anos.

O segundo destaque é o ano de 2016. Em 2016 rolou uma grande epidemia de Influenza A (H1N1), com isso, o aumento da curva de 2016 pode ser justificada.

Claramente está ocorrendo algum “fenômeno” que fez as notificações de SRAG aumentarem no ano de 2020. Com isso, temos indícios de subnotificação do COVID-19.

Figura 1 – Número de Casos ao Longo das Semanas Filtrado Pelos Anos Para a Série SRAG Brasil.

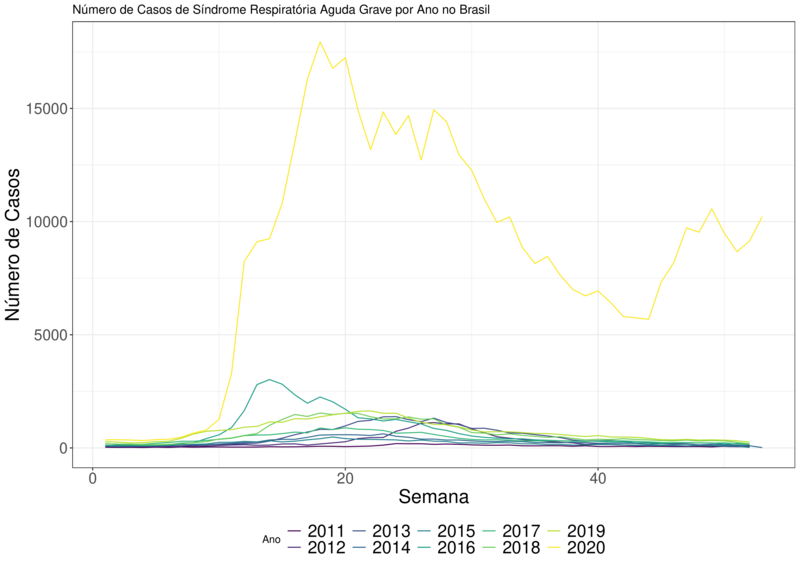
Figura 2 – Número de Casos ao Longo das Semanas Filtrado Pelos Anos Para a Série SRAG Pernambuco.

Para melhorar, ou dar mais evidências das subnotificações, foi construído um gráfico para comparar o ano de 2020 com a média histórica dos anos de 2011 a 2019. A partir disso, podemos observar nas Figuras (3) e (4) uma diferença absurdas entres as curvas.

Figura 3 – Número de Casos ao Longo das Semanas do ano 2020 em Comparação Com Média dos Anos de 2011 a 2019 para a Série SRAG Brasil.

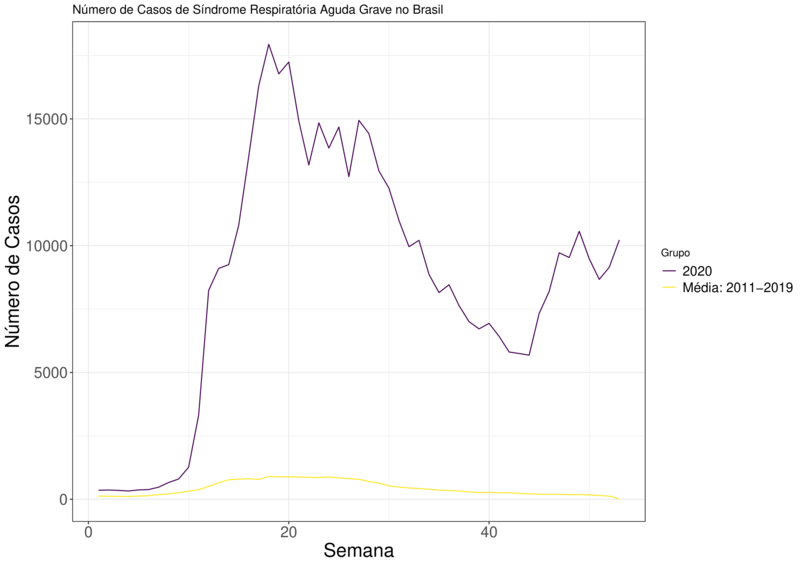
Figura 4 – Número de Casos ao Longo das Semanas do ano 2020 em Comparação Com Média dos Anos de 2011 a 2019 para a Série SRAG Pernambuco.

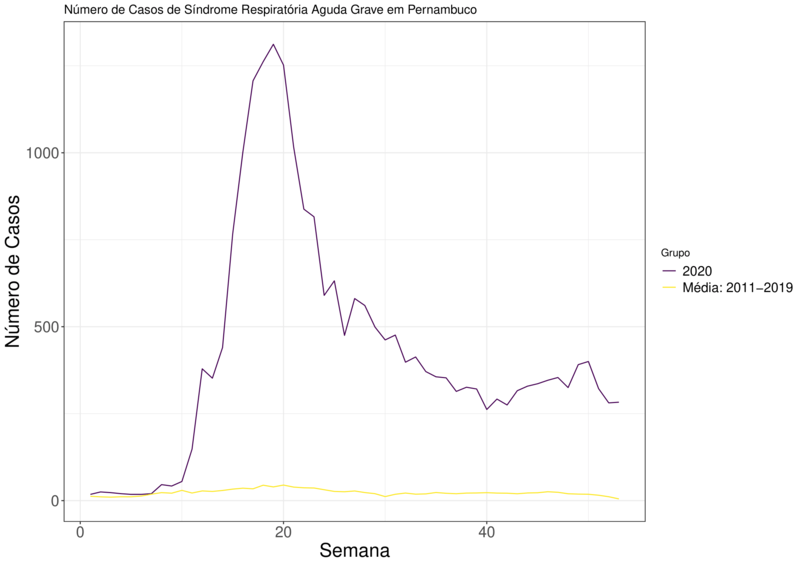
Finalizado essa breve análise, partiremos para ver o comportamento das previsões dos métodos usuais de séries temporais com a série SRAG (Brasil e Pernambuco).

Série Temporal

Para tentar fazer previsões com o máximo de fidelidade ao valor real, tentamos ajustar o algoritmo Holt-Winters e o modelo ARIMA, para ver o comportamento deles com as séries, e compará-los entre si.

A série do SRAG (Brasil e Pernambuco) com dados semanais, ao longo dos anos pode ser vista na Figura (5). Não podemos ver com clareza se as séries possui tendência ou sazonalidade, mais podemos ver com clareza, nas duas séries, uma quebra estrutural. Isso foi visto anteriormente, como indícios de subnotificações do COVID-19.

Figura 5A – Série Temporal da SARG Brasil:

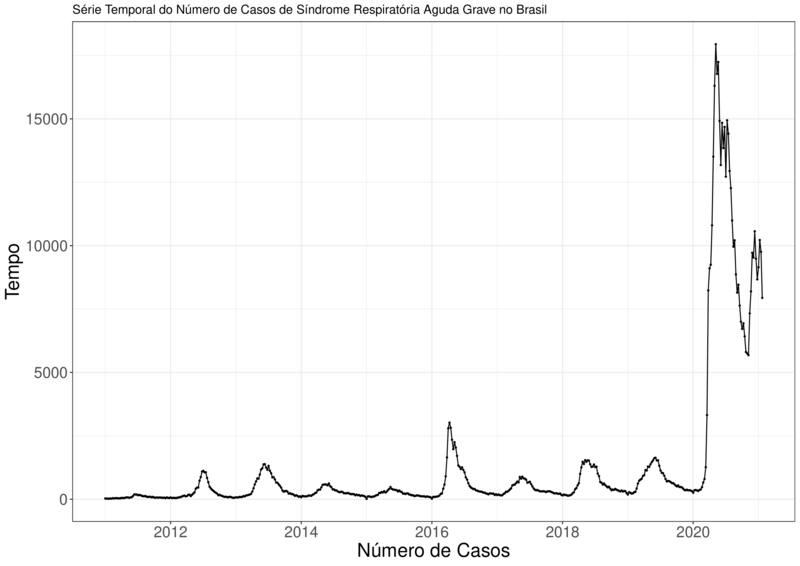
Figura 5B – Série Temporal da SARG Pernambuco:

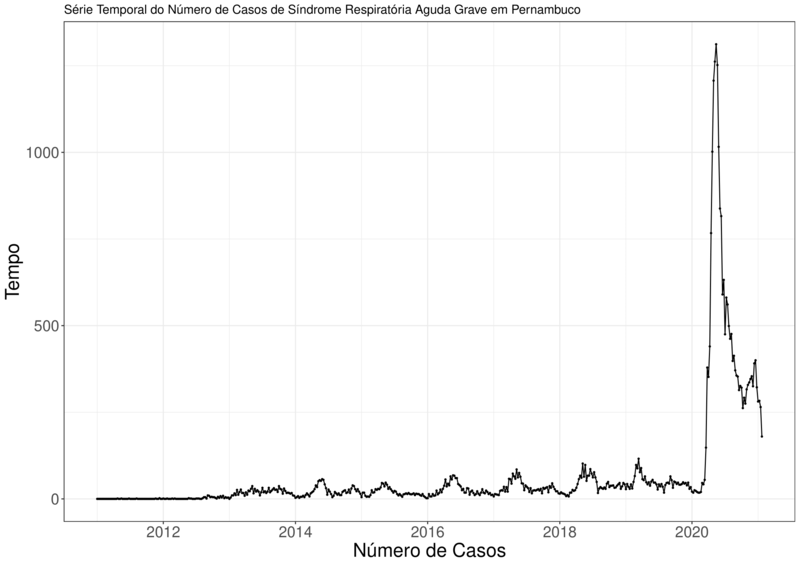
Os dois gráficos são bem parecidos, o que é normal, já que estamos apenas filtrando a base de dados do Brasil, para um único estado, Pernambuco.

Usando a média de casos por semanas ao longo do anos, é possível tentar identificar se a indícios de sazonalidade.

Figura 6A – Média de casos por Semanas ao Longo do Anos no Brasil. 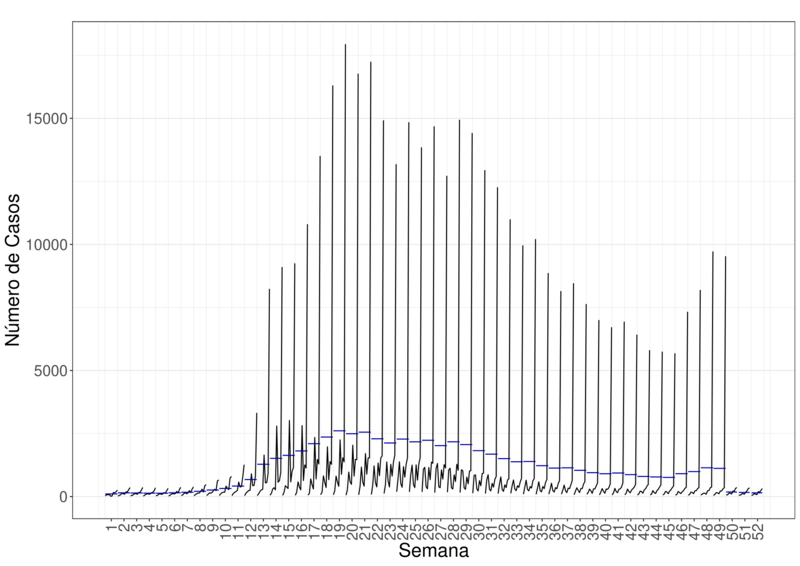Figura 6B – Média de casos por Semanas ao Longo do Anos em Pernambuco.

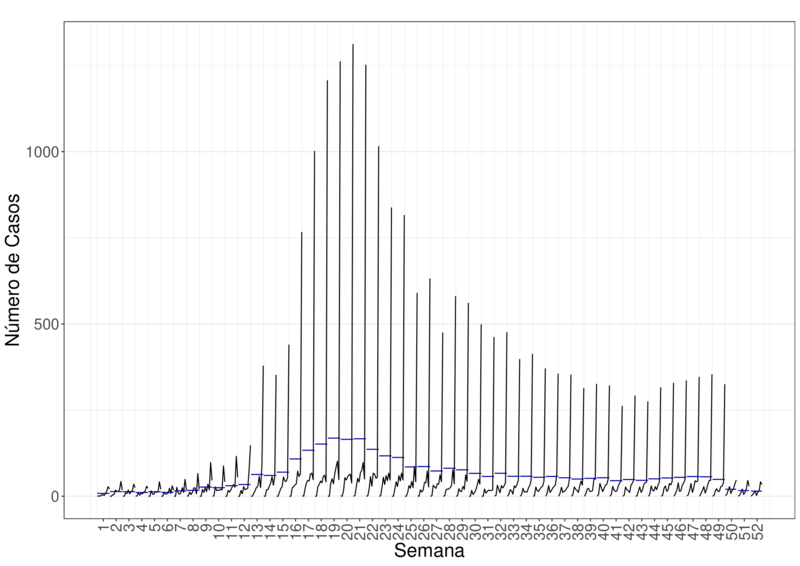
Como existe uma quebra estrutural em ambas as séries, visto na Figura (5), é possível ver uma diferença nas medinas ao longo dos anos. Porém, não é possível saber de forma visual se essa diferença é por uma sazonalidade ou pela quebra estrutural.

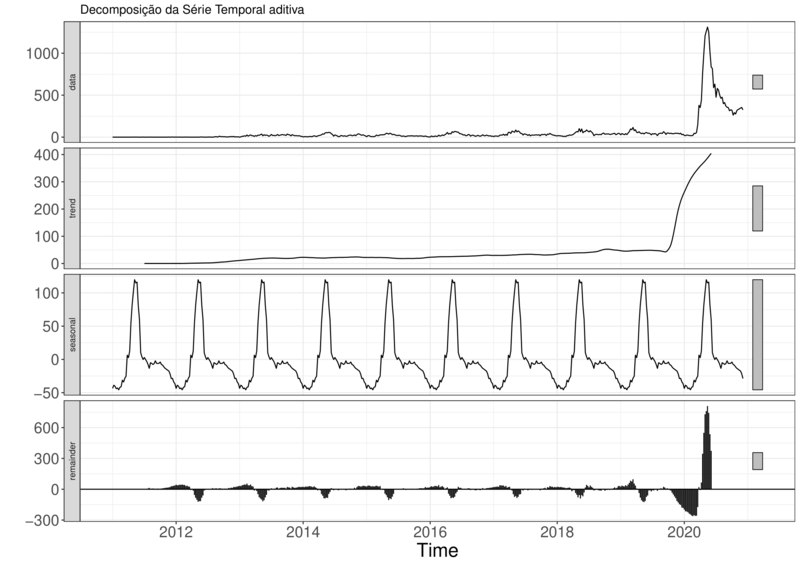
Fazendo a decomposição das séries em componentes não-observáveis, podemos perceber que não existe indícios de sazonalidade multiplicativa. Também é possível ver certa tendência em ambas as série. A decomposição das séries pode ser vista na Figura (7).

Figura 7A – Decomposição das Séries em Componentes Não-Observáveis no Brasil.

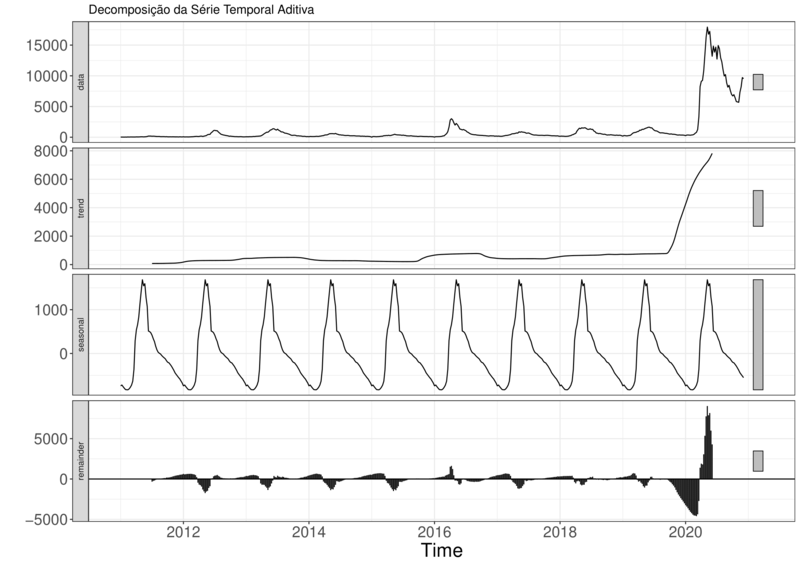
Figura 7B – Decomposição das Séries em Componentes Não-Observáveis em Pernambuco.

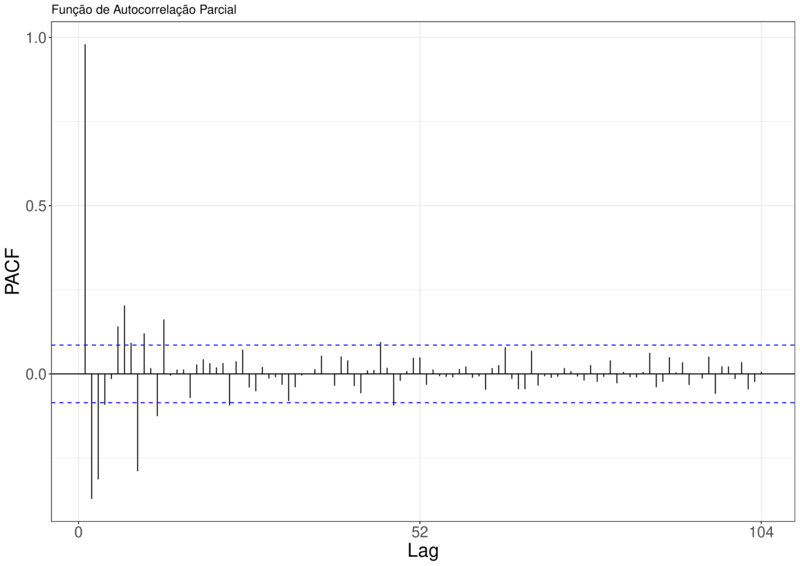
Fazendo os gráficos da função autocorrelação(ACF) e da função de autocorrelação parcial(PACF) para as séries Brasil e Pernambuco, podemos ver um decrescimento lento no Gráfico da ACF, em ambos gráficos. Dando indícios que a série tem raiz unitária e precisa ser diferenciada. Também temos indícios que a série não contém sazonalidade aleatória já que não temos alternâncias de picos no gráfico ACF.

Figura 8 – Função de Autocorrelação e Função de Autocorrelação Parcial para a Série SRAG Brasil.

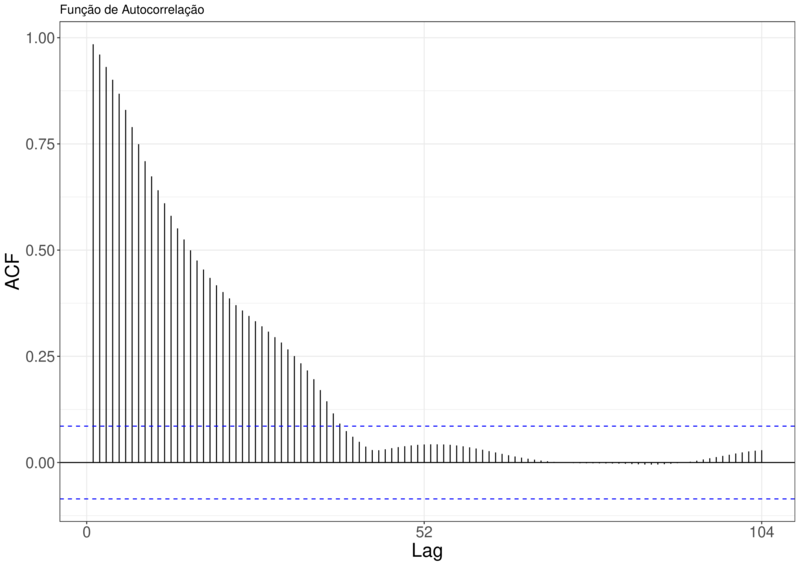
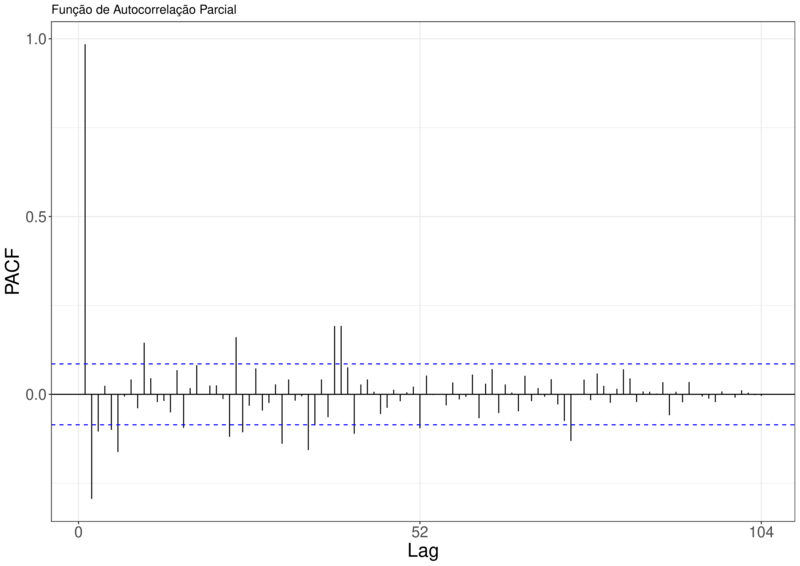
Figura 9 – Função de Autocorrelação e Função de Autocorrelação Parcial para a Série SRAG Pernambuco.

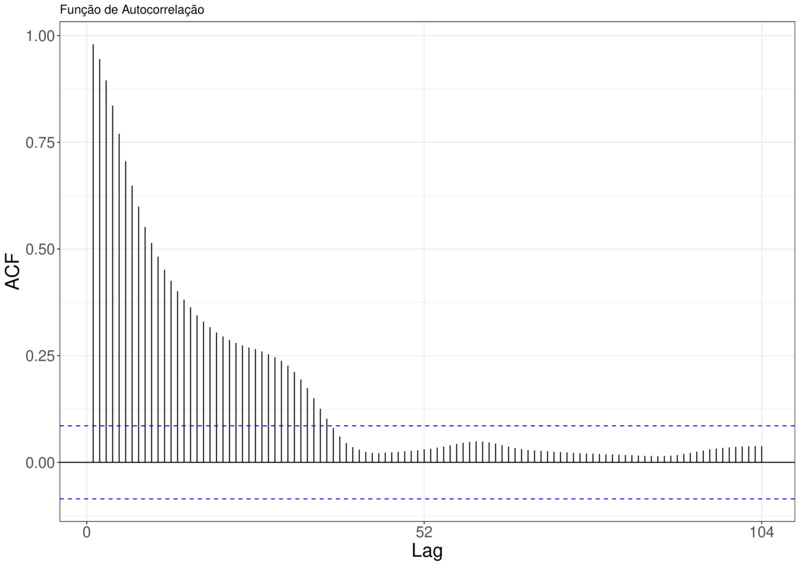
Com os indícios de raiz unitária, foi feito um teste ADF[2], onde obtemos o valor da estatística de teste

• Valor da estatística de teste para a série Brasil: $-1.5546$

• Valor da estatística de teste para a série Pernambuco: $-3.0419$

onde a região critica é dada pela Tabela (3)

Tabela 3 – Valores Críticos para o Teste ADF.

Como os dois valores da estatística de teste deram menor que o valor tabelado de $1%$, temos que as duas séries precisam ser diferenciada ao nível de $1%$.

A partir de agora, ajustaremos os métodos usuais propostos, faremos previsões, e em seguida usaremos algumas medidas de erros para verificar qual dos dois modelos obteve melhor estimativa.

Algoritmo Hotz-Winters

O primeiro método de previsão a ser usado foi a classe de algoritmos de alisamento exponencial, o algoritmo de Holt-Winters.

As estimativas dos ajustes para as duas séries podem ser vistas na Tabela (4).

Tabela 4A – Valores Estimados Para os Parâmetros de Suavização no Brasil.

Tabela 4B – Valores Estimados Para os Parâmetros de Suavização em Pernambuco.

Após as estimativas geradas a partir do algoritmo Holt-Winters, foram feitas previsões para 6 semanas em ambas as séries (Brasil e Pernambuco).

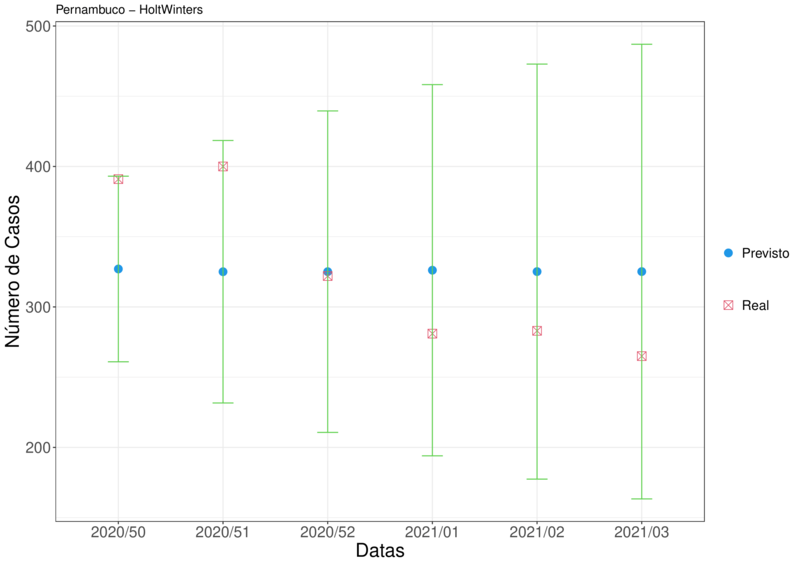
Podemos ver as previsões pelas Tabelas (5) e (6). Com ela, podemos comparar o valor previsto com o valor verdadeiro.

Tabela 5 – Previsões para as próximas 6 semanas para a série SRAG Brasil.

Tabela 6 – Previsões para as próximas 6 semanas para a série SRAG Pernambuco.

Uma observação importante, é que esses intervalos de confiança gerados não são bem definidos por serem construídos a partir da distribuição normal.

Para facilitar a visualização das Tabelas (5) e (6), foi construído dois gráficos afim de representar as mesmas.

Podemos notar pela Figura (10) que apenas um valor ficou fora do intervalo de confiança. Já na Figura (11), todos os intervalos continham o valor verdadeiro.

Figura 10 – Representação da Tabela (5)

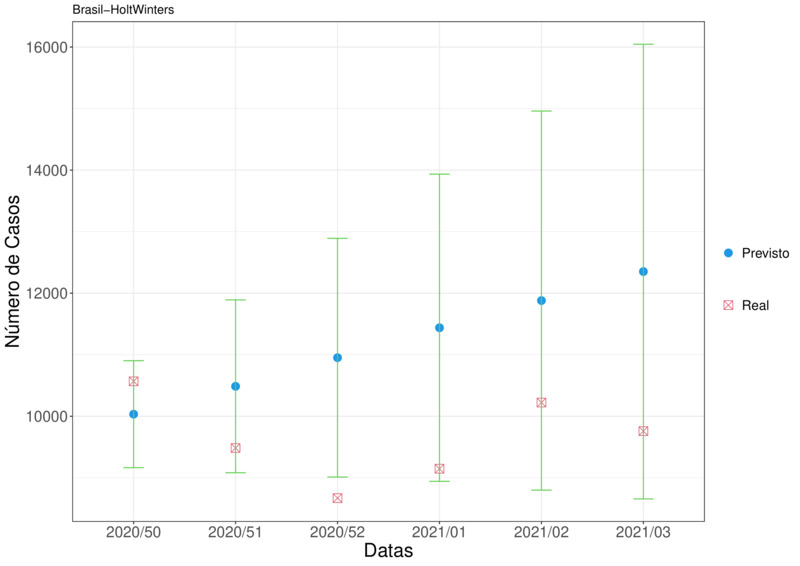
Figura 11 – Representação da Tabela (6)

Modelo ARIMA

Foram ajustados vários modelos para as séries SRAG, Brasil e Pernambuco, e os modelos escolhidos foram os que continham menor AICc[3], e que passaram na análise de diagnóstico.

Para a série SRAG Brasil, foi escolhido o modelo ARIMA(9,1,2). Como vimos anteriormente, a série continha raiz unitária e precisava ser diferenciada. As estimativas e erro padrão podem ser visto na Tabela (7).

Tabela 7 – Valores Estimados para o Modelo ARIMA(9,1,2) para a série SRAG Brasil.

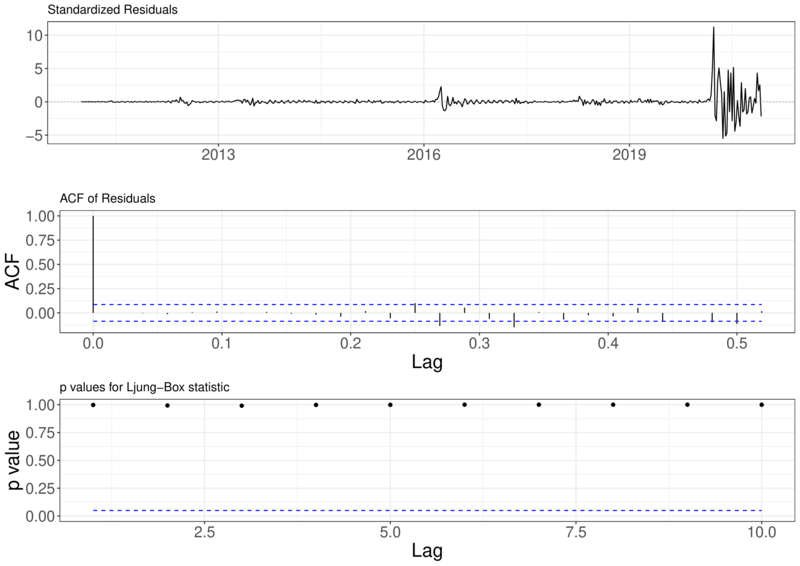
Ao fazer a análise de diagnóstico, podemos perceber pela Figura (12) que é possível ver alguns ruídos no gráfico dos erros padrões. Esses ruídos são no ano de 2016 e 2020, como falado na análise descritiva, esses anos tiveram uma epidemia e uma pandemia respectivamente.

No gráfico da ACF dos resíduos, podemos perceber que nem todos os lags estão dentro do intervalo. Porém, pelo gráfico da estatística de Ljung-Box, não temos nenhum lag significativo, mostrando assim que o modelo escolhido está ajustado.

Figura 12 – Diagnostico do Modelo ARIMA(9,1,2) para a série SRAG Brasil

Depois do ajuste e da análise de diagnostico do modelo, partiremos para as previsões das próximas seis semanas e compararemos com o valor verdadeiro da série. A Tabela (8) mostra as previsões, valor real e intervalos de confiança.

Tabela 8 – Previsões para as próximas 6 semanas para a série SRAG Brasil.

Novamente, uma observação importante é que esses intervalos de confiança gerados não são bem definidos por serem construídos a partir da distribuição normal. Para mais detalhes ver: .

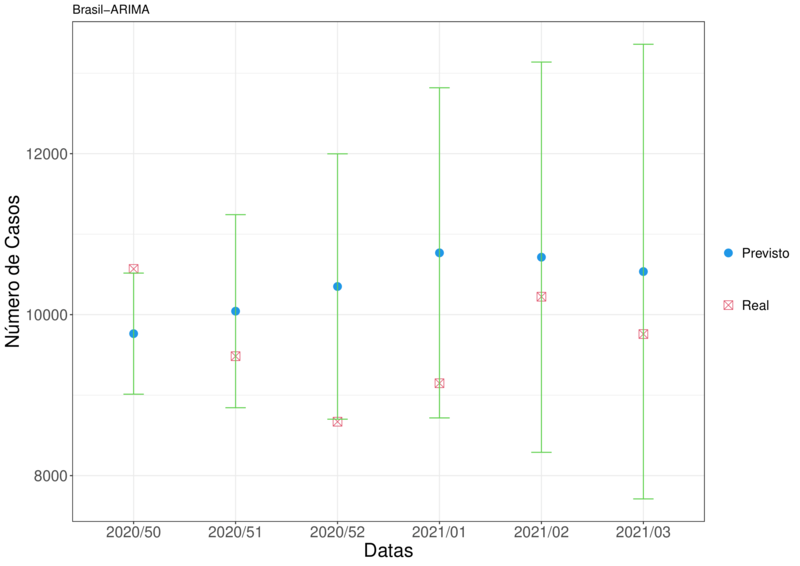
Para facilitar o entendimento da Tabela (8), foi construído um gráfico, Figura (13), para visualizar a distancia do valor real para o estimado.

Podemos perceber pela Figura (13), que apenas dois intervalos de confiança não continham o valor verdadeiro.

Figura 13 – Representação da Tabela (8)

Agora, fazendo o ajuste para a série SRAG Pernambuco, foram ajustados vários modelos, e foi escolhido o que continha menor AICc, e que passou na análise de diagnóstico.

O modelo escolhido foi um ARIMA(5,1,10). Como vimos anteriormente, a série continha raiz unitária e precisava ser diferenciada. As estimativas e erro padrão podem ser visto na Tabela (9).

**Tabela 9 – Valores Estimados para o Modelo ARIMA(5,1,10) para a série SRAG Pernambuco.

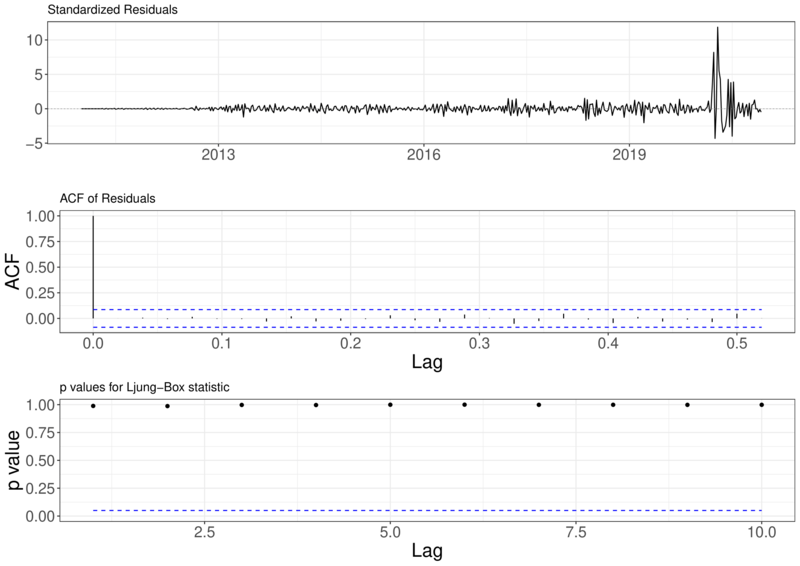
Ao fazer a análise de diagnóstico, podemos perceber pela Figura (14) que é possível ver alguns ruídos no gráfico dos erros padrões. Esses ruídos são mais notórios no ano de 2020, dando mais indícios de subnotificação do COVID-19.

No gráfico da ACF dos resíduos, não percebemos nenhum lags fora dentro do intervalo. E ainda, pelo gráfico da estatística de Ljung-Box, não temos nenhum lag significativo, mostrando assim que o modelo escolhido está ajustado.

Figura 14 – Diagnostico do Modelo ARIMA(5,1,10) para a série SRAG Pernambuco.

Depois do ajuste e da análise de diagnostico do modelo, partiremos para as previsões das próximas seis semanas e compararemos com o valor verdadeiro da série. A Tabela (10) mostra as previsões, valor real e intervalos de confiança.

Tabela 10 – Previsões para as próximas 6 semanas para a série SRAG Pernambuco.

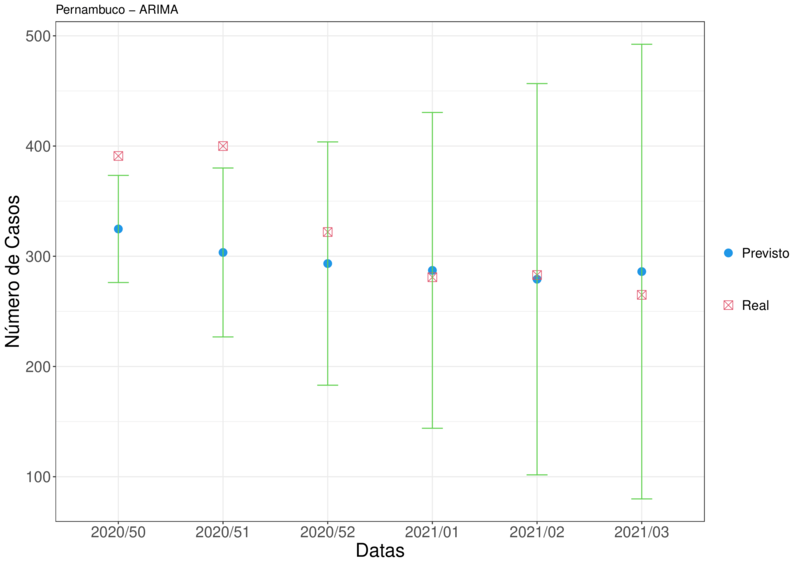
Para facilitar o entendimento da Tabela (10), foi construído um gráfico, Figura (15), para visualizar a distancia do valor real para o estimado.

Podemos perceber pela Figura (15), que apenas os dois primeiros intervalos de confiança não continham o valor verdadeiro.

Figura 15 – Representação da Tabela (10)

Comparação Holt-Winters x ARIMA

A partir de algumas medidas de erros, iremos comparar os dois métodos de previsões e definir qual se adequar melhor os dados.

As Tabelas (11) e (12) mostram algumas medidas de erro, e assim como foi mencionando anteriormente, os intervalos de confiança gerados não são bem definidos, por serem construídos a partir da distribuição normal. Com isso, as medidas de erro servem para da uma comparação e precisão dos ajustes.

Podemos perceber que tanto o RMSE e MAE do modelo ARIMA é menor que o do algoritmo de Holt-Winters, mostrando assim, que o modelo ARIMA é superior (nas séries analisadas) que o algoritmo de Holt-Winters, tanto no dados de treinamento como no de previsão.

Tabela 11A – Medidas de erro, SRAG Brasil (ARIMA).

Tabela 11B – Medidas de erro, SRAG Brasil (Holt-Winters).

Tabela 12A – Medidas de erro, SRAG Pernambuco (ARIMA).

Tabela 12B – Medidas de erro, SRAG Pernambuco (Holt-Winters).

Conclusão

Como virmos desde a análise descritiva, temos grandes indícios que existe sim subnotificações do COVID-19. Com o ajuste dos modelos, fizemos previsões das próximas seis semanas e o comparamos com o valor real. Vimos que o modelo ARIMA tem melhor ajuste, já que o mesmo contém menor erro.

Código R

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270

library(tidyverse)
theme_set(theme_bw() + theme(axis.title = element_text(size =20),
axis.text = element_text(size = 16),
legend.text=element_text(size=14)))
library(reshape2)
require(readxl)
require(dplyr)
require(ggplot2)
require(ggfortify)
require(tseries)
require(urca)
require(forecast)
require(gridExtra)
library(zoo)
library(xtable)
dados<-read.csv("Downloads/Dados_InfoGripe_serie_temporal_com_estimativas_recentes.csv",
sep = ";", dec = ",")

dados<-dados[,2:10]
names(dados)<-c("UF", "Unidade.da.Federação", "Tipo", "dado", "escala", "ano",
"epiweek","Situação.do.dado", "casos")


#### GRAFICO

srag_filtrado_brasil <- dados %>%
filter(Unidade.da.Federação=="Brasil") %>%
filter(dado=="srag") %>%
filter(escala=="casos") %>%
filter(ano >= 2011) %>%
filter(ano <= 2020)

srag_filtrado_brasil$ano<-as.factor(srag_filtrado_brasil$ano)

srag_filtrado_PE <- dados %>%
filter(Unidade.da.Federação=="Pernambuco") %>%
filter(dado=="srag") %>%
filter(escala=="casos") %>%
filter(ano >= 2011) %>%
filter(ano <= 2020)

srag_filtrado_PE$ano<-as.factor(srag_filtrado_PE$ano)

ggplot(srag_filtrado_brasil, aes(x = epiweek, y = casos,
group = ano, colour = ano)) +
geom_line() +
scale_colour_viridis_d() +
labs(x = "Semana", y = "Número de Casos", colour = "Ano",
title="Número de Casos de Síndrome Respiratória Aguda Grave por Ano no Brasil")


ggplot(srag_filtrado_PE, aes(x = epiweek, y = casos, group = ano, colour = ano)) +
geom_line() +
scale_colour_viridis_d() +
labs(x = "Semana", y = "Número de Casos", colour = "Ano",
title="Número de Casos de Síndrome Respiratória Aguda Grave por Ano em Pernambuco")


srag_medio_BR <- srag_filtrado_brasil %>%
filter(ano != "2020") %>%
group_by(epiweek) %>%
summarise(media = mean(casos))

full_join(srag_medio_BR, filter(srag_filtrado_brasil, ano == "2020")) %>%
select(epiweek, media, casos) %>%
melt(id.var="epiweek") %>%
mutate(variable = ifelse(variable == "media", "Média: 2011-2019", "2020")) %>%
ggplot(., aes(x = epiweek, y = value, group = variable, colour = variable)) +
geom_line() +
scale_colour_viridis_d() +
labs(x = "Semana", y = "Número de Casos", colour = "Grupo",
title="Número de Casos de Síndrome Respiratória Aguda Grave no Brasil")


srag_medio_PE <- srag_filtrado_PE %>%
filter(ano != "2020") %>%
group_by(epiweek) %>%
summarise(media = mean(casos))

full_join(srag_medio_PE, filter(srag_filtrado_PE, ano == "2020")) %>%
select(epiweek, media, casos) %>%
melt(id.var="epiweek") %>%
mutate(variable = ifelse(variable == "media", "Média: 2011-2019", "2020")) %>%
ggplot(., aes(x = epiweek, y = value, group = variable, colour = variable)) +
geom_line() +
scale_colour_viridis_d() +
labs(x = "Semana", y = "Número de Casos", colour = "Grupo",
title="Número de Casos de Síndrome Respiratória Aguda Grave em Pernambuco")

#### SERIE TEMPORAL

srag_filtrado_brasil_completa <- dados %>%
filter(Unidade.da.Federação=="Brasil") %>%
filter(dado=="srag") %>%
filter(escala=="casos") %>%
filter(ano >= 2011)
srag_filtrado_brasil_completa<-srag_filtrado_brasil_completa[1:524,]

srag_filtrado_PE_completa <- dados %>%
filter(Unidade.da.Federação=="Pernambuco") %>%
filter(dado=="srag") %>%
filter(escala=="casos") %>%
filter(ano >= 2011)
srag_filtrado_PE_completa<-srag_filtrado_PE_completa[1:524,]

serie_brasil_completa<-ts(srag_filtrado_brasil_completa$casos,
start = c(2011,1),frequency = 52)

serie_brasil_treino<-window(serie_brasil_completa,
start = c(2011,1),end=c(2020,49))

serie_brasil_teste<-window(serie_brasil_completa,
start=c(2020,50))

serie_PE_completa<-ts(srag_filtrado_PE_completa$casos,
start = c(2011,1),frequency = 52)

serie_PE_treino<-window(serie_PE_completa,start = c(2011,1),
end=c(2020,49))

serie_PE_teste<-window(serie_PE_completa,start=c(2020,50))

autoplot(serie_brasil_completa, xlab = "Número de Casos",
ylab = "Tempo",
main = "Série Temporal do Número de Casos de Síndrome Respiratória Aguda Grave no Brasil") +
geom_point(size=0.5) + scale_colour_viridis_d()

autoplot(serie_PE_completa,xlab = "Número de Casos",
ylab = "Tempo", main = "Série Temporal do Número de Casos de Síndrome Respiratória Aguda Grave em Pernambuco")+
geom_point(size=0.5) + scale_colour_viridis_d()

ggtsdisplay(serie_brasil_completa)
ggtsdisplay(serie_PE_completa)

ggAcf(serie_brasil_completa, main = "Função de Autocorrelação")
ggPacf(serie_brasil_completa, main = "Função de Autocorrelação Parcial")


ggAcf(serie_PE_completa, main = "Função de Autocorrelação")
ggPacf(serie_PE_completa, main = "Função de Autocorrelação Parcial")


serie_brasil_treino %>% decompose() %>%
autoplot(main="Decomposição da Série Temporal Aditiva")

serie_brasil_treino %>% ur.df() %>% summary()
serie_brasil_treino %>% ggsubseriesplot() +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))+
labs(x = "Semana", y = "Número de Casos",
title="")

serie_PE_treino %>% decompose() %>%
autoplot(main="Decomposição da Série Temporal aditiva")


serie_PE_treino %>% ur.df() %>% summary()
serie_PE_treino %>% ggsubseriesplot() +
theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1))+
labs(x = "Semana", y = "Número de Casos",
title="")


ajuste_brasil<-auto.arima(serie_brasil_treino,
stepwise = F,
trace = T,
max.p = 10,
max.q = 10,
max.P = 2,
max.Q = 2,
max.D = 1,
d=1,
max.order = 20)

ggtsdiag(ajuste_brasil)

ajuste_PE<-auto.arima(serie_PE_treino,
stepwise = F,
trace = T,
max.p = 10,
max.q = 10,
max.P = 2,
max.Q = 2,
max.D = 1,
d=1,
max.order = 20
)


ggtsdiag(ajuste_PE)


previsao_BR<-forecast(ajuste_brasil,6)
previsao_PE<-forecast(ajuste_PE,6)

## HoltWINTERS

ajuste_brasil_A<-HoltWinters(serie_brasil_treino, seasonal = "additive")
ajuste_PE_A<-HoltWinters(serie_PE_treino, seasonal = "additive")

previsao_BR_A<-forecast(ajuste_brasil_A,6)
previsao_PE_A<-forecast(ajuste_PE_A,6)


previsao_BR_A
previsao_PE_A

###
dadoss<-as.data.frame(previsao_BR)
dadoss$real<-as.vector(serie_brasil_teste[-7])
dadoss$data<-c("2020/50","2020/51","2020/52","2021/01","2021/02","2021/03")

names(dadoss)<-c("Forecast","Lo80","Hi80","Lo95","Hi95","Real","Point")
ggplot(dadoss, aes(x=Point, y=Forecast)) +
geom_point(aes(shape='Previsto'),color=4,size=4)+
geom_point(aes(x=Point, y=Real,fill='Real'), color=2, shape = 7, size=4)+
geom_errorbar(aes(ymin=Lo95, ymax=Hi95), width=.2,color=3) +
ggtitle('Brasil-ARIMA')  + ylab("Número de Casos") + xlab("Datas") +
guides(shape=guide_legend(title="")) +
guides(fill=guide_legend(title=""))

dadoss<-as.data.frame(previsao_BR_A)
dadoss$real<-as.vector(serie_brasil_teste[-7])
dadoss$data<-c("2020/50","2020/51","2020/52","2021/01","2021/02","2021/03")

names(dadoss)<-c("Forecast","Lo80","Hi80","Lo95","Hi95","Real","Point")
ggplot(dadoss, aes(x=Point, y=Forecast)) +
geom_point(aes(shape='Previsto'),color=4,size=4)+
geom_point(aes(x=Point, y=Real,fill='Real'), color=2, shape = 7, size=4)+
geom_errorbar(aes(ymin=Lo95, ymax=Hi95), width=.2,color=3) +
ggtitle('Brasil-HoltWinters')  + ylab("Número de Casos") + xlab("Datas") +
guides(shape=guide_legend(title="")) +
guides(fill=guide_legend(title=""))


#######

dadoss<-as.data.frame(previsao_PE)
dadoss$real<-as.vector(serie_PE_teste[-7])
dadoss$data<-c("2020/50","2020/51","2020/52","2021/01","2021/02","2021/03")

names(dadoss)<-c("Forecast","Lo80","Hi80","Lo95","Hi95","Real","Point")
ggplot(dadoss, aes(x=Point, y=Forecast)) +
geom_point(aes(shape='Previsto'),color=4,size=4)+
geom_point(aes(x=Point, y=Real,fill='Real'), color=2, shape = 7, size=4)+
geom_errorbar(aes(ymin=Lo95, ymax=Hi95), width=.2,color=3) +
ggtitle('Pernambuco - ARIMA')  + ylab("Número de Casos") + xlab("Datas") +
guides(shape=guide_legend(title="")) +
guides(fill=guide_legend(title=""))

dadoss<-as.data.frame(previsao_PE_A)
dadoss$real<-as.vector(serie_PE_teste[-7])
dadoss$data<-c("2020/50","2020/51","2020/52","2021/01","2021/02","2021/03")

names(dadoss)<-c("Forecast","Lo80","Hi80","Lo95","Hi95","Real","Point")
ggplot(dadoss, aes(x=Point, y=Forecast)) +
geom_point(aes(shape='Previsto'),color=4,size=4)+
geom_point(aes(x=Point, y=Real,fill='Real'), color=2, shape = 7, size=4)+
geom_errorbar(aes(ymin=Lo95, ymax=Hi95), width=.2,color=3) +
ggtitle('Pernambuco - HoltWinters')  + ylab("Número de Casos") + xlab("Datas") +
guides(shape=guide_legend(title="")) +
guides(fill=guide_legend(title=""))


#####

accuracy(previsao_BR,serie_brasil_teste)
accuracy(previsao_BR_A,serie_brasil_teste)

accuracy(previsao_PE,serie_PE_teste)
accuracy(previsao_PE_A,serie_PE_teste)