Desempenho e concordância entre alguns testes De normalidade sob a presença e ausência de outliers.

20-02-2019 3939 words 19 minutes

Contents

Este trabalho foi apresentado no Conapesc 2019, e teve orientação da Prof. Dr. Amanda dos Santos Gomes, amanda.natalia.gomes@gmail.com.

Temos como objetivo mostrar o desempenho dos mais populares testes de normalidade para dados com e sem a presença de outliers e verificar o nível de concordância dos testes nestes tipos de situações. De maneira geral, verificou-se que o teste de Jarque-Bera é o mais poderoso nas amostras com a presença de outliers. O teste teve o melhor desempenho para pequenas e grandes amostras. Nas amostras sem a presença de outliers, o teste de Shapiro-Wilk foi o mais poderoso seguido do Shapiro-Francia. Aplicou-se o coeficiente Kappa-Fleiss para avaliar a concordância na tomada de decisão. Para amostras com outliers os testes apresentaram baixa concordância e para amostras sem outliers os testes apresentaram forte concordância.

Introdução

No dia a dia das pessoas que trabalham com dados amostrais ou experimentais é bastante comum a suposição de normalidade dos dados, isso porque é uma condição exigida para a realização de muitas inferências válidas a respeito de parâmetros populacionais.

A distribuição normal é um modelo probabilístico contínuo, sendo um dos mais importantes, pois a maioria dos métodos estatísticos são baseados nesse modelo e muitos fenômenos aleatórios podem ser descritos de forma aproximada por ele.

Na inferência há vários pressupostos a serem observados, os pressupostos estatísticos mais considerados são normalidade, linearidade e homoscedasticidade. Este trabalho focará apenas no pressuposto de normalidade visto que exige-se por inúmeros procedimentos estatísticos, tais como: construção de intervalos de confiança, testes de hipóteses, análise de variância e modelagem estatística. Assim, torna-se importante verificar esse pressuposto antes de se prosseguir com os procedimentos estatísticos que o exijam.

O software R disponibiliza diversas maneiras de verificar a normalidade dos dados, sendo eles, métodos gráficos, métodos numéricos e os testes de normalidade. O mais famoso método gráfico é o QQ-plot, no qual o mesmo imprime os pontos sobre uma reta afim de avaliar sua normalidade, sendo porém uma técnica subjetiva. Assim, para se obter uma conclusão formal é importante efetuar um teste estatístico.

A motivação para este trabalho surgiu a partir do interesse de avaliar o desempenho dos testes de normalidade de Shapiro-Wilk, Anderson-Darling, Lilliefors, Jarque-Bera, Shapiro-Francia e Cramer-von Mises para dois tipos situações: A primeira para dados sem a presença de outliers e a segunda com a presença de outliers. O desempenho será realizado a partir das análises da taxas de erro tipo I e poder empírico.

Metodologia

Neste trabalho foram consideradas algumas estratégias para avaliar as taxas do erro do tipo I, poder e concordância entre esses testes. Foi utilizada a simulação de Monte Carlo, e em cada simulação foram aplicados os testes de normalidade em um nível de significância pré-estabelecido de 5%, sendo verificado se a hipótese nula, de que os dados seguem uma distribuição normal, foi ou não rejeitada.

Caso tenha sido rejeitada a hipótese nula e a amostra tenha sido gerada da distribuição normal, foi cometido um erro do tipo I. Da mesma forma se a hipótese nula for rejeitada e a amostra foi obtida de uma população não-normal, uma decisão correta foi tomada.

Em cada caso, foi repetido 10.000 vezes e a proporção de decisões incorretas no primeiro caso é a taxa de erro tipo I e no segundo caso, a proporção de decisões corretas é o poder empírico do teste.

Os testes de Anderson-Darling, Lilliefors, Shapiro-Francia e Cramer-von Mises foram aplicados utilizando as funções, ad.test(), lilli.test(), sf.test() e cvm.test(), respectivamente. Todas essas funções são encontradas no pacote nortest. O teste de Shapiro-Wilk foi aplicado utilizando-se a função shapiro.test() do pacote stats, e o teste Jarque-Bera com função jb.norm.test() do pacote normtest.

Desenvolvimento

Simulação Monte Carlo

Foram realizados dois experimentos, o primeiro com 10.000 replicas de Monte Carlo sob as hipóteses $H_0$ e $H_1$, de diversas distribuições de probabilidade, em que foi produzido de cada distribuição, amostras de tamanho n, nos quais esses valores foram: 10, 20, 30, 50, 100, 200, 300, 500 e 1.000. E no segundo experimento foi adotada a mesma ideia do primeiro, porém, todas as distribuições geradas continham outliers.

Erro tipo I

Foram simuladas 10.000 amostras aleatórias normais de tamanhos $n$ com a função rnorm, com média 0 e desvio padrão 1.

Se, ao aplicar os testes, a hipótese nula de normalidade é rejeitada a um nível de significância de 5%, então a distribuição dos dados é considerada erroneamente como não-normal. A proporção de rejeições incorretas foi calculada para cada teste e representam as taxas de erro tipo I.

Poder

Foram simuladas amostras aleatórias de distribuições não-normal para avaliar o poder dos testes, que é rejeitar a hipótese nula que por construção é falsa.

Em dois experimentos, 10.000 amostras de tamanho $n$ de algumas distribuições não-normais, simétricas e assimétricas, foram simuladas. No primeiro sem a presença de outliers, e no segundo com a presença de outliers.

As distribuições simétricas foram a uniforme(0,1), beta(2,2) e t-student(10). Já as distribuições assimétricas foram Gamma(2,1), $\chi^2$(15), lognormal(0,1), exponencial(1) e weibull(2,1).

As distribuições foram simuladas por meio das funções random do software R.

Os testes de normalidade foram aplicados em cada uma das 10.000 amostras de cada distribuição simulada e a proporção de rejeições corretas da hipótese nula foi computada. Os valores obtidos representam o poder dos testes que foram comparados entre si.

Concordância

Os dados foram computados para cada uma das distribuições com n tamanhos diferentes. Foi feito um coeficiente Kappa-Fleiss com função Kappam.fleiss do pacote irr, para verificar o nível concordância entre os testes na tomada de decisão entre rejeitar ou não a hipótese nula de normalidade. A concordância foi aplicado apenas nas amostras não provenientes da distribuição normal. Com isso, verificaremos se o poder dos testes interfere diretamente na concordância.

Resultados e Discussões

Nesta seção serão apresentados os resultados das simulações para obtenção do erro do tipo I, poder e concordância dos testes de normalidade.

Sem a Presença de Outliers

Foram avaliados seis testes de normalidade, Anderson-Darling, Lilliefors, Shapiro-Francia, Cramer-von Mises, Shapiro-Wilk e Jarque-Bera. A Tabela [1] apresenta as taxas de erro tipo I para diferentes tamanhos amostrais.

Tabela 1: Erro do tipo I das amostras sem outliers dos testes Anderson-Darling (AD), Lilliefors (LL), Shapiro-Francia (SF), Cramer-von Mises (CVM), Shapiro-Wilk (SW) e Jarque- Bera (JB)

Tamanho	SW	AD	CVM	LL	SF	JB
10	0,0466	0,0442	0,0424	0,0478	0,0506	0,0484
15	0,0482	0,0502	0,0496	0,0472	0,0528	0,0548
20	0,0496	0,0500	0,0500	0,0506	0,0496	0,0476
30	0,0544	0,0520	0,0514	0,0470	0,0514	0,0514
50	0,0460	0,0512	0,0542	0,0546	0,0482	0,0456
100	0,0512	0,0506	0,0498	0,0530	0,0520	0,0532
200	0,0528	0,0524	0,0530	0,0484	0,0524	0,0480
300	0,0478	0,0480	0,0434	0,0454	0,0488	0,0484
500	0,0514	0,0450	0,0482	0,0472	0,0504	0,0474
1000	0,0496	0,0468	0,0460	0,0470	0,0520	0,0500

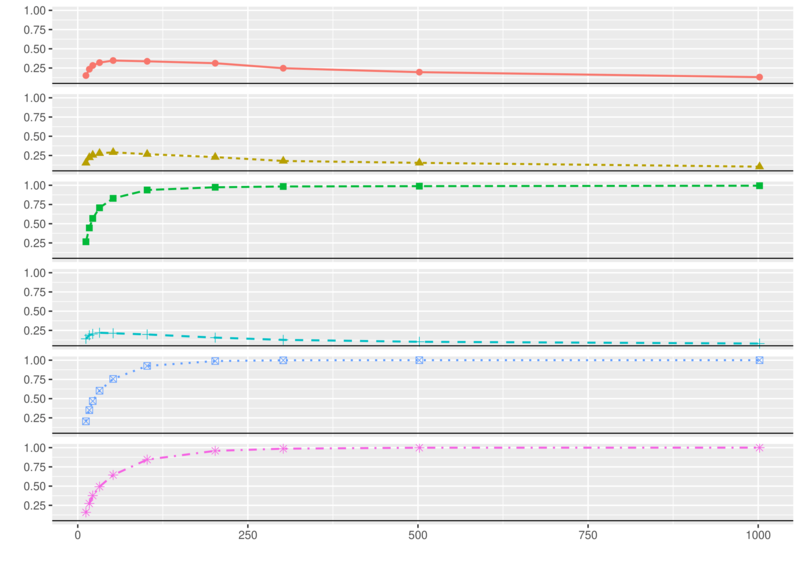
As duas Figuras abaixo são a representação da Tabela 1.

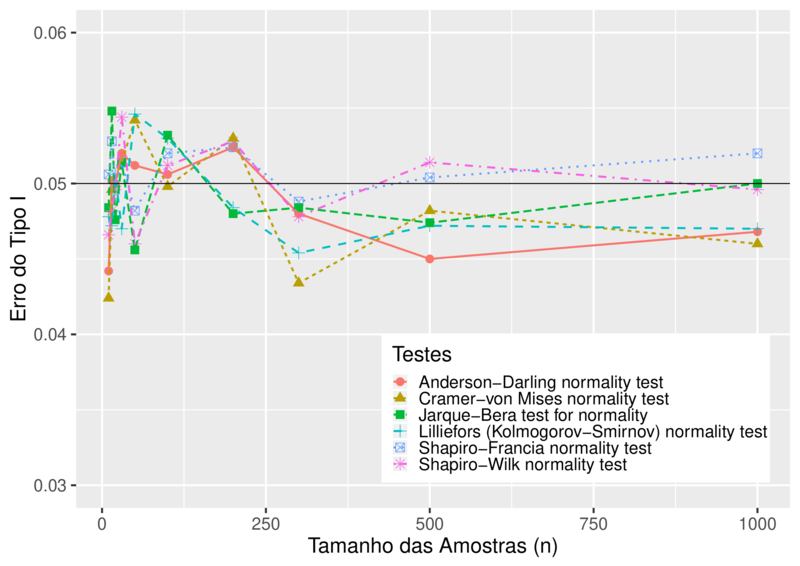
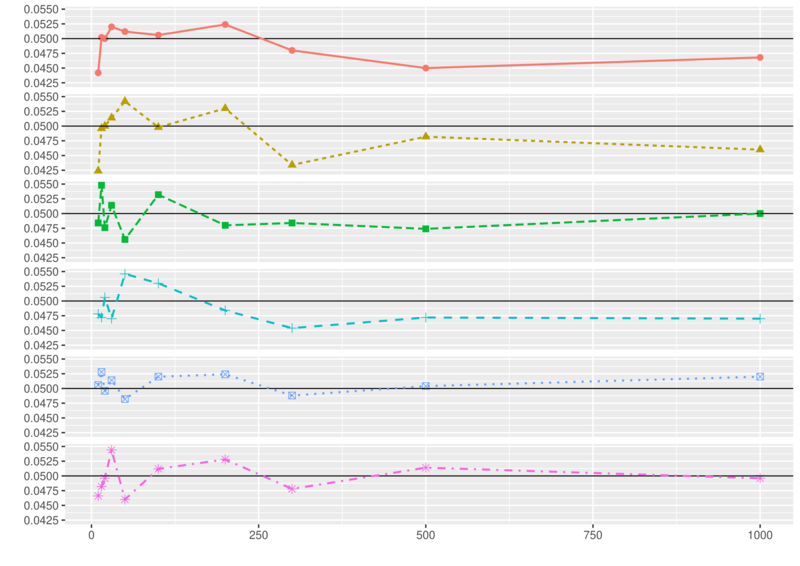
Por meio das duas Figuras acima e da Tabela 1 verificou-se que a taxa de erro do tipo I, para todos os testes, oscilou consideravelmente em torno do valor nominal de 5%, para amostras pequenas, $n\leq 30$. Ainda pela Figura 1, nota-se que a medida que o tamanho da amostra aumenta, os testes de Shapiro-Francia e Shapiro-Wilk vão se aproximando mais rápido da taxa nominal de 0,05 tornando-os assim testes mais precisos. O teste Jarque-Bera tende a rejeitar menos à hipótese nula de normalidade, pois a maioria das suas oscilações estão abaixo do nível nominal de 0,05. O teste de Shapiro-Francia pouco oscila sobre o valor nominal, o tornando um dos testes mais precisos para calcular o erro do tipo I. Os testes de Anderson-Darling, Lilliefors e Cramer-von Mises, são os menos precisos, ficando distantes do valor nominal. Já o teste de Shapiro-Wilk, é mais poderoso entre eles tendo baixas oscilações em torno do valor nominal.

Pela Tabela 2 podemos observar a variância dos testes em relação ao valor nominal para todas as amostras. Nas Tabelas 3 e 4 podemos observar para pequenas e grandes amostras, respectivamente.

Tabela 2: Variância para todos tamanhos amostrais

SW	AD	CVM	LL	SF	JB
$6,400 \times 10^{-7}$	$1,024 \times 10^{-5}$	$1,600 \times 10^{-5}$	$1,547 \times 10^{-5}$	$7,471 \times 10^{-6}$	$3,004 \times 10^{-6}$

Tabela 3: Variância para pequenas amostras $n \leq 30$

SW	AD	CVM	LL	SF	JB
$4,800 \times 10^{-7}$	$4,320 \times 10^{-6}$	$1,452\times 10^{-5}$	$1,825\times 10^{-5}$	$6,453 \times 10^{-6}$	$1,613\times 10^{-6}$

Tabela 4: Variância para grandes amostras $n \geq 50$

SW	AD	CVM	LL	SF	JB
$2,048 \times 10^{-6}$	$3,200 \times 10^{-6}$	$3,200 \times 10^{-6}$	$1,095 \times 10^{-5}$	$5,408 \times 10^{-6}$	$7,200 \times 10^{-6}$

Percebe-se que o teste de Shapiro-Wilk seguido do Shapiro-Francia foram os mais precisos de uma forma geral. Porém, para pequenas amostras o teste de Shapiro-Francia perde a segunda colocação para o teste Jarque-Bera, já que mesmo teve menor variância.

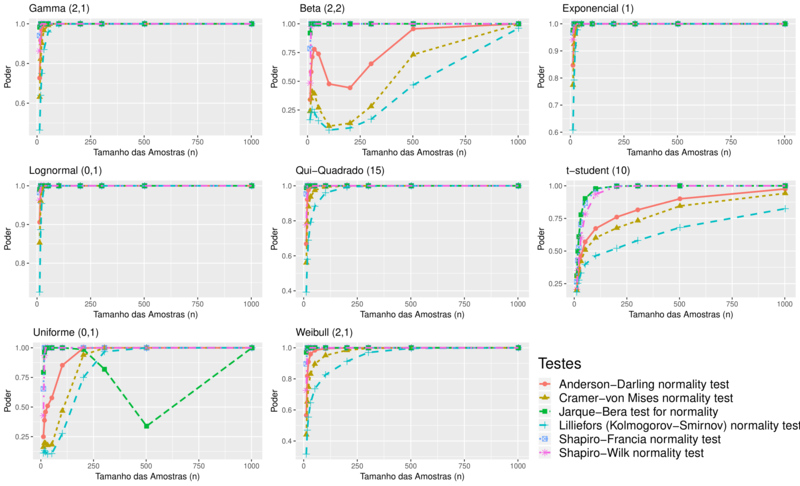
Na Figura abaixo encontramos o poder de cada teste para as distribuições simétricas e assimétricas, com diferentes tamanhos amostrais.

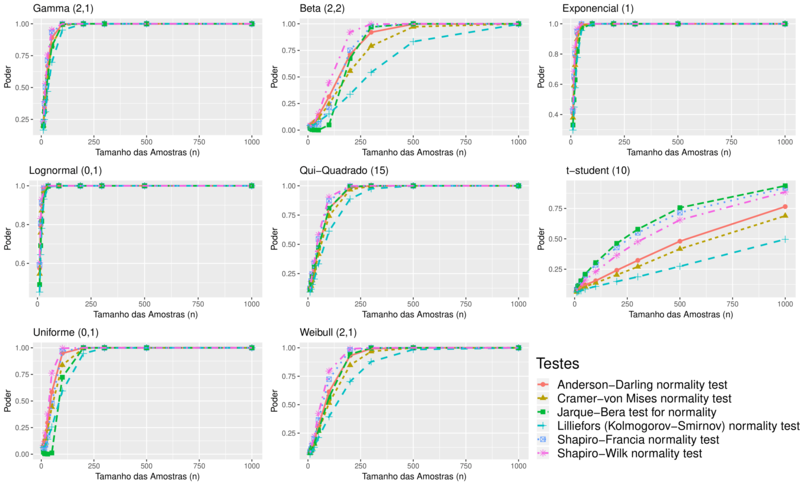
Para amostras provenientes da distribuição uniforme e beta, percebe-se que o teste de Shapiro-Willk tem um comportamento melhor quando se trata de amostras pequenas, seguido do teste de Anderson-Darling. Em relação aos demais testes, o teste Jarque-Bera apresentou o menor poder nas distribuições uniforme e beta para amostras pequenas, para amostras maiores que 150 o teste de Lilliefors apresentou menor poder.

Para a distribuição t-student os testes diferem bastante quanto ao poder, mesmo para o maior tamanho amostral. A dificuldade dos testes em identificar corretamente a falta de normalidade quando os dados seguem a distribuição t-student se deve ao fato das duas distribuições possuírem densidades muito parecidas. Levando em consideração todos os tamanhos amostrais, o teste que melhor identificou os dados provenientes da distribuição t-student foi o Jarque-Bera, seguido do teste Shapiro-Francia. O teste Lilliefors apresentou o menor poder na distribuição t-student.

Nas distribuições assimétricas o teste mais poderoso foi o de Shapiro-Wilk, seguido do Shapiro-Francia. Nas distribuições weibull e $\chi^2$, os mesmos se destacaram para amostras menores que 250, ou seja, para pequenas amostras o poder dos testes de Shapiro-Wilk e Shapiro-Francia se destacaram em relação aos outros. Todos os testes tiveram poder máximo com amostras maiores que 500, exceto pelo teste de Lilliefors, que novamente ficou com menor poder em comparação com os outros testes.

Em oposição a isso, tem-se os testes apresentaram ótimos resultados de poder para as distribuições, lognormal, exponencial e gamma. Mesmo assim, os testes de Shapiro-Wilk e Shapiro-Francia foram superiores em todos os casos.

Coeficiente kappa para amostras sem outliers

Pela Tabela 5 temos todos os resultados do coeficiente kappa para as diferentes distribuições mencionadas anteriormente. Percebe-se que para a maioria das distribuições, os testes tiveram forte concordância entre rejeitar ou não a hipótese de normalidade. Porém, as distribuições beta, $\chi^2$ e t-student obtiveram menor concordância. Isso pode ser visto na Figura acima onde os testes tem menor precisão na identificação não normalidade. Isso se deve ao fato das distribuições possuírem densidades muito parecidas.

Tabela 5: Coeficiente Kappa

Gamma	Beta	Exponencial	Lognormal	$\chi^2$	t-student	Uniforme	Weibull
0,90	0,38	0,93	1,00	0,66	0,40	0,86	0,81

Com a presença de outliers

A seguir serão apresentados os resultados das simulações com a presença de outliers para obtenção do erro do tipo I, poder e concordância dos testes de normalidade. Em cada amostra foram adicionados dois outliers, sendo um 10% do valor mínimo e o outro 100% do valor máximo.

Tabela 6: Erro do tipo I das amostras com outliers dos testes Anderson-Darling (AD), Lilliefors (LL), Shapiro-Francia (SF), Cramer-von Mises (CVM), Shapiro-Wilk (SW) e Jarque- Bera (JB)

Tamanho	SW	AD	CVM	LL	SF	JB
10	0,16	0,15	0,15	0,14	0,20	0,27
15	0,27	0,23	0,22	0,19	0,35	0,45
20	0,38	0,28	0,26	0,20	0,47	0,57
30	0,49	0,32	0,28	0,22	0,60	0,71
50	0,64	0,35	0,29	0,21	0,76	0,83
100	0,84	0,34	0,27	0,20	0,93	0,94
200	0,96	0,31	0,23	0,16	0,99	0,97
300	0,99	0,25	0,18	0,13	1,00	0,98
500	1,00	0,20	0,15	0,10	1,00	0,99
1000	1,00	0,13	0,10	0,08	1,00	0,99

De forma geral, todos os testes apresentaram dificuldades em identificar a normalidade dos dados com a presença de outliers. Pelas Figura abaixo, nota-se que os testes são sensíveis com a presença de outliers se distanciando bastante do valor nominal de 0,05.

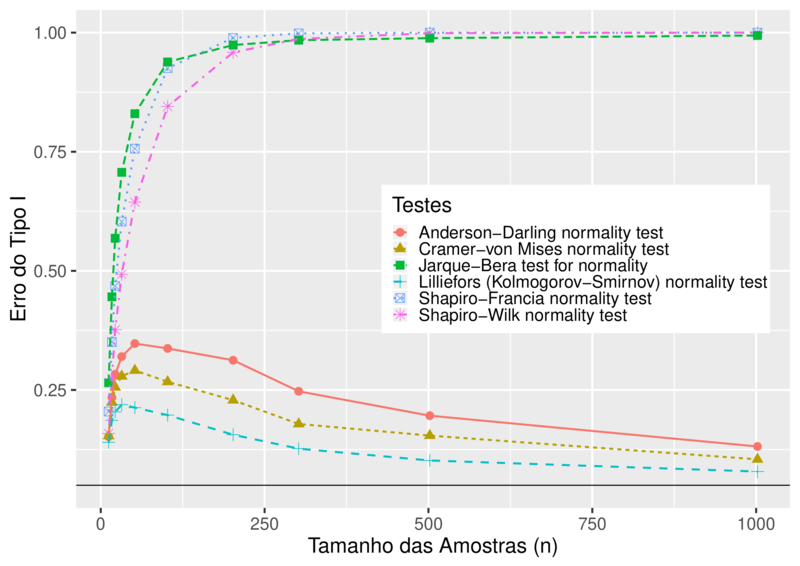
Os testes de Anderson-Darling, Lilliefors e Cramer-von Mises foram os menos sensíveis aos outliers, obtendo melhor desempenho se aproximando do valor nominal de acordo com a Tabela 6.

Pela Tabela 7 podemos observar a variância dos testes em relação ao valor nominal para todas as amostras. Nas Tabelas 8 e 9 podemos observar para pequenas e grandes amostras.

Tabela 7: Variância para todos tamanhos amostrais

SW	AD	CVM	LL	SF	JB
4,313	0,472	0,295	0,142	5,138	5,760

Tabela 8: Variância para pequenas amostras $n \leq 30$

SW	AD	CVM	LL	SF	JB
0,4033333	0,2028	0,1680333	0,1008333	0,6721333	1,08

Tabela 9: Variância para grandes amostras $n \geq 50$

SW	AD	CVM	LL	SF	JB
6,20498	0,4805	0,2645	0,1125	7,03298	7,34472

Percebe-se que os testes de Anderson-Darling, Cramer-von Mises e Lilliefors foram os mais precisos de uma forma geral. Para pequenas e grandes amostras o teste de Lilliefors ficou com a menor variância, seguido do teste de Cramer-von Mises. O teste Jarque-Bera foi o mais sensível de todos tendo uma alta variação.

O poder para as distribuições simétricas e assimétricas geradas com a presença de outliers, pode ser observado pela Figura 6.

Para amostras provenientes da distribuição uniforme, percebe-se que o teste Jarque-Bera tem o melhor comportamento quando se trata de amostras pequenas, seguido do teste de Shapiro-Francia. A partir de amostras maiores que 250, o teste mais poderoso foi o de Shapiro-Francia, seguido do Shapiro-Wilk. Os mesmos se tornam melhores opções, pois não há oscilações como o teste Jarque-Bera. Em relação aos demais testes, o teste de Lilliefors apresentou menor poder.

Nas amostras provenientes da distribuição beta, o teste Jarque-Bera tem o melhor poder para amostras pequenas. O mesmo ganha poder rapidamente seguido do teste Shapiro-Francia. Os demais testes apresentaram oscilações a medida que as amostras aumentam, porém, essas oscilações tendem a ser crescentes tornando os testes mais poderosos. O teste de Lilliefors mais uma vez, foi o menos poderoso, mesmo para grandes amostras.

Para amostras com outliers provenientes da distribuição t-student, os testes seguem com a mesma dificuldade apresentadas na seção anterior. A dificuldade dos testes em identificarem corretamente a falta de normalidade dos dados se deve ao fato das duas distribuições possuírem densidades muito parecidas. Em consideração a todos os tamanhos amostrais, o teste com melhor desempenho na distribuição t-student com a presença de outliers foi o Jarque-Bera, seguido do teste Shapiro-Francia. O teste Lilliefors apresentou o menor poder na distribuição t-student.

Nas amostras provenientes das distribuições gamma, exponencial, lognormal e $\chi^2$ os testes apresentaram ótimos resultados de poder, inclusive o teste de Lilliefors. Mesmo assim, os testes de Shapiro-Wilk e Shapiro-Francia foram superiores em todos os casos.

Coeficiente Kappa para amostras com outliers

Pela Tabela 10 temos todos os resultados do coeficiente kappa para as diferentes distribuições com a presença de outliers. Percebe-se que quase todas as distribuições, os testes tiveram fraca concordância entre rejeitar ou não a hipótese de normalidade. Porém, as distribuições exponencial e lognormal obtiveram concordância máxima. As outras distribuições tiveram fraca concordância, isso pode ser visto na Figura acima, onde os testes tem menor precisão na identificação da normalidade.

Tabela 10: Coeficiente Kappa

Gamma	Beta	Exponencial	Lognormal	$\chi^2$	t-student	Uniforme	Weibull
0,43	0,06	1	1	0,37	0,52	0,15	0,19

Considerações finais

Para dados de distribuição normal sem a presença de outliers, os testes avaliados foram bem precisos tendo pouca variação em torno do valor nominal de 5%, onde os melhores testes para a taxa de erro tipo I foram o Shapiro-Wilk seguido do Shapiro-Francia. Em relação aos dados de distribuição normal com a presença de outliers, os melhores testes para a taxa de erro tipo I foram o Lilliefors seguido do Cramer-von Mises. Vale ressaltar as dificuldades de todos os testes para amostras com a presença de outliers os mesmos tiveram alta variação em relação ao valor nominal.

Em relação ao poder, os testes de Shapiro-Wilk seguido do Shapiro-Francia tiveram melhor desempenho para as distribuições geradas sem a presença de outliers, tornando-os testes mais poderosos/adequados para esse tipo de dados. Nas distribuições geradas com a presença de outliers, o teste Jarque-Bera foi o que obteve melhor desempenho seguido do teste de Shapiro-Wilk.

R

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491



library(nortest)
library(normtest)
library(moments)

alpha=0.05
m<-10000

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL


for(i in 1:m){
  amostra <- rbeta(10,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp10.txt', row.names = FALSE)


###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(15,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp15.txt', row.names = FALSE)



###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(20,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp20.txt', row.names = FALSE)


###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(30,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp30.txt', row.names = FALSE)



###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(50,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp50.txt', row.names = FALSE)

###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(100,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp100.txt', row.names = FALSE)

###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(200,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp200.txt', row.names = FALSE)


###########################################################################################################

shap<-NULL
and<-NULL
cvm<-NULL
lilli<-NULL
sf<-NULL
jb<-NULL



for(i in 1:m){
  amostra <- rbeta(300,2,2)
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)


  shap[i]<-a$p.value
  and[i]<-b$p.value
  cvm[i]<-c$p.value
  lilli[i]<-d$p.value
  sf[i]<-e$p.value
  jb[i]<-f$p.value


}

power.shapiro<-mean(shap<alpha)
power.ad<-mean(and<alpha)
power.cvm<-mean(cvm<alpha)
power.lillie<-mean(lilli<alpha)
power.sf<-mean(sf<alpha)
power.jbr<-mean(jb<alpha)


poder<-c(power.shapiro,power.ad,power.cvm,power.lillie,power.sf,power.jbr)

testedenormalidade<-function(amostra,alpha){
  a<-shapiro.test(amostra)
  b<-ad.test(amostra)
  c<-cvm.test(amostra)
  d<-lillie.test(amostra)  
  e<-sf.test(amostra)  
  f<-jb.norm.test(amostra)

  nomes<-c(a$method,b$method,c$method,d$method,e$method,f$method)
  pvalores<-c(a$p.value,b$p.value,c$p.value,d$p.value,e$p.value,f$p.value)
  tamanho<-rep(length(amostra),length(pvalores))

  return(data.frame(Testes= nomes ,Pvalor = pvalores, RejeitaH0=ifelse(pvalores<=alpha,'SIM','NAO'),Poder = poder, Tamanho=tamanho))
}

save<-testedenormalidade(amostra,alpha)

write.csv(save, 'exp300.txt', row.names = FALSE)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53



####


library(ggplot2)
library(gridExtra)
library(grid)



d10<-read.table('exp10.txt',header = T, sep = ',')
d15<-read.table('exp15.txt',header = T, sep = ',')
d20<-read.table('exp20.txt',header = T, sep = ',')
d30<-read.table('exp30.txt',header = T, sep = ',')
d50<-read.table('exp50.txt',header = T, sep = ',')
d100<-read.table('exp100.txt',header = T, sep = ',')
d200<-read.table('exp200.txt',header = T, sep = ',')
d300<-read.table('exp300.txt',header = T, sep = ',')
d500<-read.table('exp500.txt',header = T, sep = ',')
d1000<-read.table('exp1000.txt',header = T, sep = ',')


grafico<-cbind(d10,d15,d20,d30,d50,d100,d200,d300,d500,d1000)
attach(grafico)

a<-ggplot(grafico,aes(x=Tamanho, y= Poder, colour= Testes,shape=Testes)) + geom_point(size=4) + geom_line(aes(linetype=Testes),size=1)  + xlab("Tamanho das Amostras (n)") + ylab("Poder")
a<-a+theme_grey(base_size = 22)
a<-a + theme(legend.position=c(0.7, 0.2))

d<-ggplot(grafico,aes(x=Tamanho, y= Poder, colour= Testes,shape=Testes)) + geom_point(size=3)  + geom_line(aes(linetype=Testes),size=1) + xlab("Tamanho das Amostras (n)") + ylab("Poder") + facet_grid(Testes ~ .) +theme_grey(base_size = 15)
d<-d + theme(strip.text = element_blank(),legend.position="none")

d10<-read.table('exp10out.txt',header = T, sep = ',')
d15<-read.table('exp15out.txt',header = T, sep = ',')
d20<-read.table('exp20out.txt',header = T, sep = ',')
d30<-read.table('exp30out.txt',header = T, sep = ',')
d50<-read.table('exp50out.txt',header = T, sep = ',')
d100<-read.table('exp100out.txt',header = T, sep = ',')
d200<-read.table('exp200out.txt',header = T, sep = ',')
d300<-read.table('exp300out.txt',header = T, sep = ',')
d500<-read.table('exp500out.txt',header = T, sep = ',')
d1000<-read.table('exp1000out.txt',header = T, sep = ',')


grafico<-rbind(d10,d15,d20,d30,d50,d100,d200,d300,d500,d1000)
attach(grafico)

a<-ggplot(grafico,aes(x=Tamanho, y= Poder, colour= Testes,shape=Testes)) + geom_point(size=4) + geom_line(aes(linetype=Testes),size=1)  + xlab("Tamanho das Amostras (n)") + ylab("Poder")
a<-a+theme_grey(base_size = 22)
a<-a + theme(legend.position=c(0.7, 0.2))

d<-ggplot(grafico,aes(x=Tamanho, y= Poder, colour= Testes,shape=Testes)) + geom_point(size=3)  + geom_line(aes(linetype=Testes),size=1) + xlab("Tamanho das Amostras (n)") + ylab("Poder") + facet_grid(Testes ~ .) +theme_grey(base_size = 15)
d<-d + theme(strip.text = element_blank(),legend.position="none")