Classificação não supervisionada no contexto não euclidiano.
Este trabalho foi apresentado no CNMAC e Conapesc 2022, e teve orientação da Prof. Dr. Getúlio José Amorim Do Amaral, gjaa@de.ufpe.br.
Em diversas ocasiões, em análise estatística de forma, é necessário agrupar um conjunto de dados em grupos, de tal maneira, que se tenha grupos com características mais homogêneas. Com isso, ter algoritmos que trabalhem no espaço não euclidiano, como é no caso dos dados de forma ou tamanho e forma, é necessário.
Classificação Não Supervisionada
Algoritmos de agrupamento por particionamento encontram uma partição que maximiza ou minimiza algum critério numérico. Este trabalho tenta adaptar para os dados de tamanho e forma, o algoritmo $K$-médias proposto por .
Uma descrição do algoritmo $K$-médias introduzido por , usa uma partição inicial e depois o valor médio dos objetos em um grupo como o protótipo de partição.
Ao trabalharmos com dados de tamanho e forma, a distância, normalmente Euclidiana, é substituída pela distância de procrustes no espaço de tamanho e forma, e ela é dada pela Equação abaixo:
$$ d_S (Y_1, Y_2) = \sqrt{S_1^2 + S_2^2 - 2S_1S_2 \cos \rho(Y_1,Y_2)}$$
em que $S_1$, $S_2$ são os tamanhos dos centroides de $Y_1$, $Y_2$, e $\rho$ é a distância Riemannian. Para mais detalhes veja minha dissertação.
A medida de dissimilaridade utilizada no $K$-médias, é a soma dos quadrados totais. A mesma modificada para os dados de tamanho e forma é definida como: $$ J= \sum_{m=1}^{\pi_m} \sum_{n=1}^{n_m} d_S(Y_{mn},\mu_{m})$$ em que $Y_{mn}$ é o $n$-ésima observação do grupo $m$ e $\mu$ é a média do grupo.
Com isso, o algoritmo $K$-médias para tamanho e forma tem os seguintes passos:
| $K$-means modificado para dados de tamanho e forma |
|---|
| Passo 1: Dados de Entrada |
| 1.1 Seja $\Omega = 1,…, n$ um conjunto de dados descrito pela matriz de configuração $\mathbf{Y}$. |
| 1.2 Calcule os dados de tamanho e forma $\mathbf{Y_C}$. |
| 1.3 Escolha $K$ centroides e gere uma partição inicial $\pi_K$ |
| 1.4 Fixe o número de iterações $T=100$ e um erro $\varepsilon > 0$; Faça $t = 1$. |
| 1.5 Calcule as médias $\mu_{K_t}$ dos grupos $\pi_{K_t}$. |
| Passo 2: Atribuindo os objetos aos grupos |
| 2.1 Calcule a distância de cada objeto em relação a média $\mu_{K_t}$ e atribua esse objeto ao novo grupo $\pi_{K_{t+1}}$ mais próximo. |
| 2.1 Calcule as médias dos novos grupos $\pi_{K_{t+1}}$ formados. |
| Passo 3: Critério de Parada |
| 3.1 Se |$\pi_{K_{t+1}} - \pi_{K_{t}}|< \varepsilon$ ou $t>T$, então Pare. Caso contrário, faça $t=t+1$ e volte para o passo $2$. |
Validação do Cluster
A validade de um estudo refere-se a quão bem os resultados encontrados representam resultados verdadeiros para indivíduos semelhantes fora do estudo. Este conceito de validade se aplica a todos os tipos de estudos, seja ele clínicos, sobre prevalência, associações, intervenções e diagnóstico. A validade de um estudo de pesquisa inclui dois domínios: a validade interna e a validade externa.
Índice Interno
A validade interna é definida como a extensão em que os resultados observados representam uma possível verdade para a população. Em nosso trabalho, usaremos o índice residual de Procrustes, já que o mesmo é muito utilizado em análise estatística de forma. Para mais detalhes veja minha dissertação.
O Índice Residual Procrustes é útil para encontrar o número ideal de grupos, e também avaliar a qualidade do ajuste em um conjunto de dados em análise estatística de formas.
Após obter a alocação dos indivíduos do conjunto de dados pelo o algoritmo $K$-médias. Calcula-se a norma quadrática dos resíduos de cada indivíduo dentro do seu grupo $(r_{in})$ e fora do seu grupo $(r_{out})$.
Com isso, o índice residual Procrustes $pr(i)$ para cada indivíduo do conjunto de dados é dado como
$$pr(i) = \frac{r_{out} (i) -r_{int} (i)}{\max(r_{out} (i),r_{int} (i))}$$
em que $-1 \leq pr(i) \leq 1$. Valores próximos de $1$ indicam que o indivíduo $i$ possui dissimilaridade menor dentro do grupo comparando com outro grupo, logo o indivíduo está agrupado apropriadamente. Valores negativos ou próximos de $-1$ indicam que o indivíduo $i$ pode ter sido alocado no grupo errado.
Para se obter um índice de validação geral de Procrutes, é feito a média de todos os $pr(i)$: $$PR = \frac{1}{n} \sum_{i=1}^{n} pr(i)$$
Uma Tabela de interpretação para os resultados do $PR$, é baseada na tabela de interpretação do índice silhueta, que pode ser visto Aqui.
Índice Externo
Feito por , o índice Rand ou medida Rand em estatística, é uma medida da similaridade entre agrupamentos de dados. Do ponto de vista matemático, o índice de Rand está relacionado à precisão, mas é aplicável mesmo quando os rótulos de classe não são usados.
Denotado por $R$, o índice Rand é calculado como: $$ R=\frac{a+b}{C_{n,2}}$$
em que, $a$, é o número de vezes que um par de elementos pertence ao mesmo cluster; $b$ é o número de vezes que um par de elementos pertence a grupos de diferentes; e $C_{n,2}$ é número de pares não ordenados em um conjunto de $n$ elementos.
Valores próximos de $1$ indicam que o agrupamento está bem definido, logo foi agrupado apropriadamente. Valores próximos de $0$ indicam que o agrupamento pode ter sido definido de forma errada.
Acurácia
Quando se fala em tecnologia atualmente, um termo que tem se tornado cada vez comum é o da acurácia. Usada muitas vezes quase como um sinônimo de precisão e eficiência. Em outras palavras, a acurácia serve para ver a porcentagem de acertos do algoritmo de agrupamento.
Aplicação e Resultados
Para verificar o comportamento do algoritmo proposto, foram criados dados artificiais de tamanho e forma contendo dois grupos. Nesses dados simulados, gerados a partir da distribuição normal complexa central, propomos dois cenários possíveis: O primeiro para grupos homogêneos e o segundo para dois grupos heterogêneo.
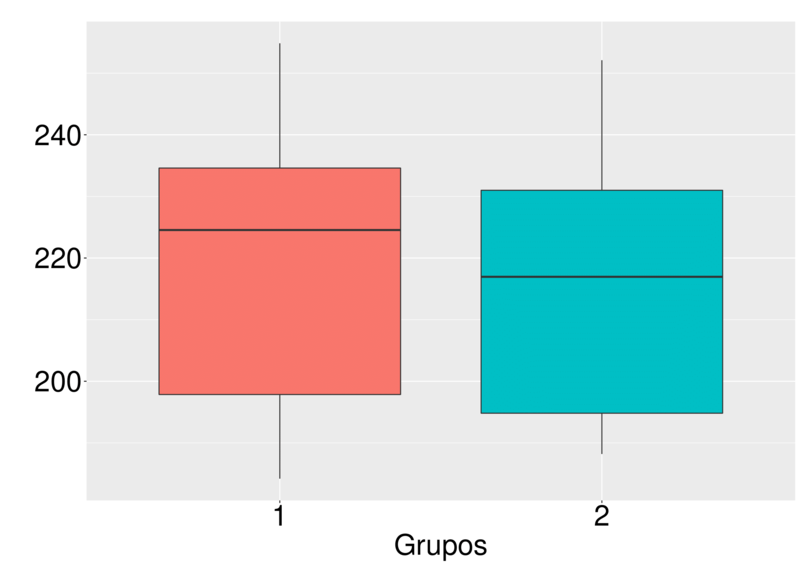
Cenário 1: grupos homogêneos.
No primeiro cenário, ao construirmos o tamanho dos centroides de cada grupo, podemos ver o quanto eles são semelhantes. Neste cenário, o algoritmo teve um pouco de dificuldade para realizar o agrupamento. Porém, seus índices interno e externos, além da acurácia, comprovam que o algoritmo teve boa performance.
| Índice de Rand | Índice de Procrustes | Acurácia | |
|---|---|---|---|
| $K$-médias | 0,809 | 0,495 | 89,58% |
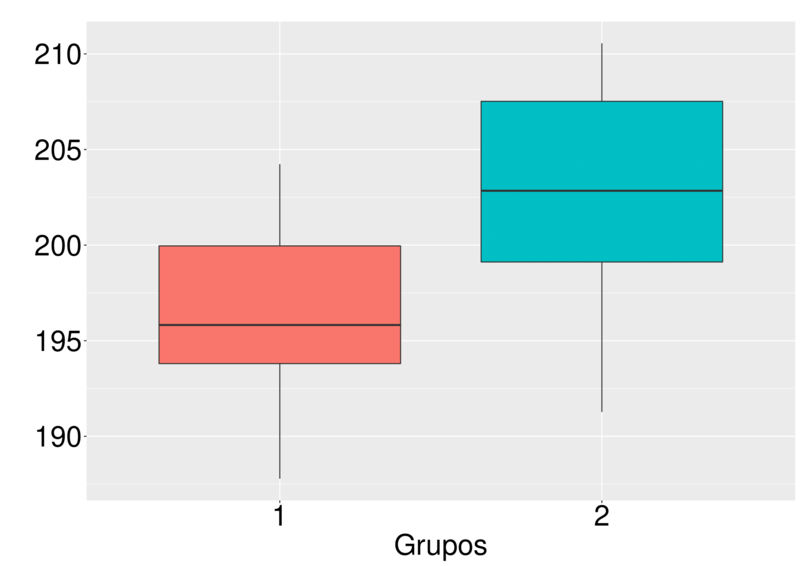
Cenário 2: grupos heterogêneo.
No segundo cenário, ao construirmos o tamanho dos centroides de cada
grupo, podemos ver que os grupo são bastantes diferentes. Nesse cenário, o algoritmo teve melhor desempenho
se comparado ao primeiro cenário.
| Índice de Rand | Índice de Procrustes | Acurácia | |
|---|---|---|---|
| $K$-médias | 0,958 | 0,627 | 97,92% |
Com isso, concluímos que à medida que o tamanho dos centroides dos grupos diferem, o algoritmo vai tendo mais facilidade em realizar o agrupamento. Além disso, provamos que o algoritmo é eficiente para tratar dados de tamanho e forma.
Dados Reais
Após a validação com os dados artificiais, aplicaremos o algoritmo
$K$-médias modificado para duas bases de dados reais. As mesmas podem
ser encontradas no pacote shapes do software
Vértebras torácicas T2 de camundongos.
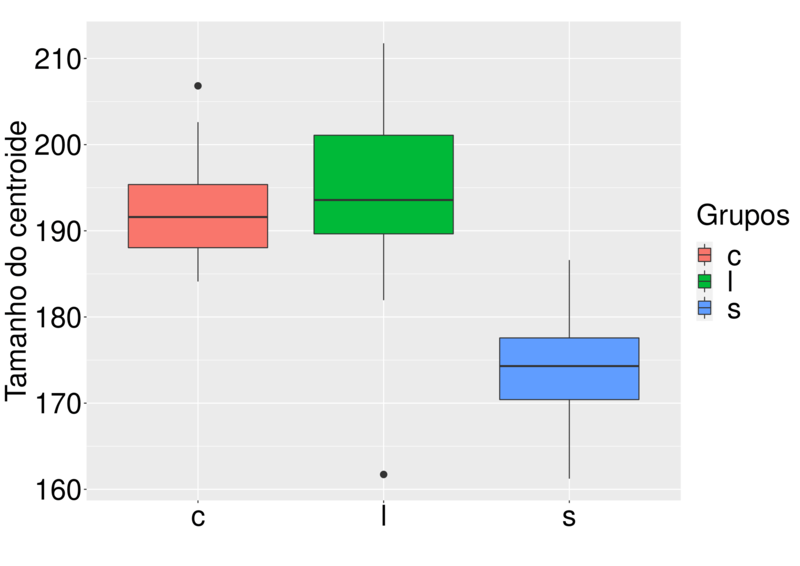
A base de dados das vértebras torácicas T2 de camundongos possui 6 marcos em 2 dimensões, e possui um total de 76 indivíduos. Esses indivíduos foram classificados em 3 grupos: controle(c)=30, grandes(l)=23 e pequenos(s)=23. Os 6 pontos de referência foram obtidos usando um método semi-automático em pontos de alta curvatura, em que, é mostrado com mais detalhes aqui.
Para ter uma ideia inicial de como os algoritmos se comportarão, foi feito o boxplot do tamanho dos centroides de cada grupo. Pela Figura abaixo, podemos ver que apenas um grupo difere dos demais, além da presença de outliers em dois grupos. Com isso, podemos supor a partir dos resultados dos dados simulados, que o algoritmo terá uma boa performance para realizar os agrupamentos.
A Tabela abaixo mostra os resultados do algoritmo, com ela, podemos ver que os resultados a performance de cada índice. De modo geral, os índices interno e externo de validação tiveram bons resultados, indicando assim que os agrupamentos foram bem definidos e posteriormente, validando os agrupamentos.
| Índice de Rand | Índice de Procrustes | Acurácia | |
|---|---|---|---|
| $K$-médias | 0,737 | 0,592 | 75,0% |
Ressonância magnética de pessoas com esquizofrenia
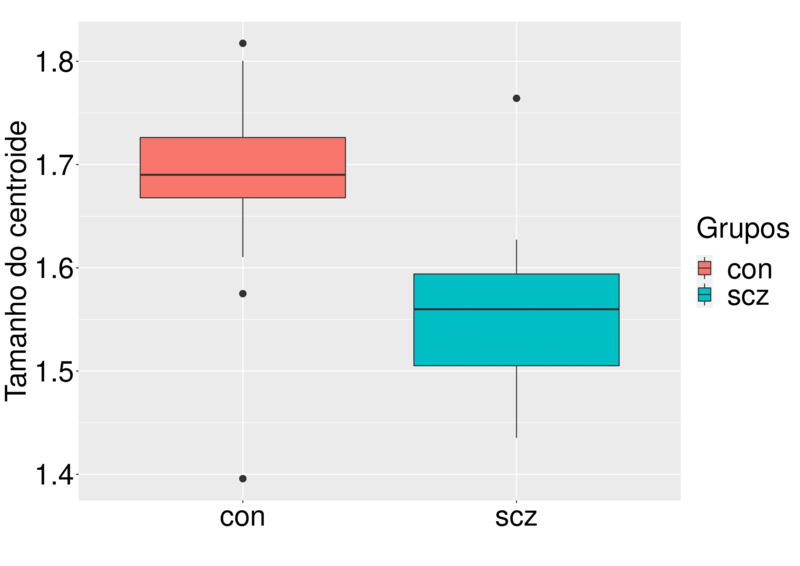
A esquizofrenia é um transtorno mental grave que muda o modo como a pessoa pensa, sente e se comporta socialmente. A base de dados das ressonâncias magnéticas de pessoas com esquizofrenia possui 13 marcos em 2 dimensões, e possui um total de 28 indivíduos. Esses indivíduos foram classificados em 2 grupos: controle(con)=14 e esquizofrênico(scz)=14. Para mais detalhes sobre a base de dados, ver .
Novamente, para ter uma ideia inicial de como os algoritmos se comportarão, foi feito o boxplot do tamanho dos centroides de cada grupo. Pela Figura abaixo, podemos ver que os dois grupos estão bem separados, porém, existe a presença de outliers nos dois grupos. Com isso, podemos supor a partir dos resultados dos dados simulados, que os algoritmos terão uma boa performance para realizar os agrupamentos.
A Tabela abaixo mostra os resultados do algoritmo, com ela, novamente, podemos ver que os resultados e a performance de cada índice. Os índices interno e externo de validação tiveram bons resultados, indicando assim que os agrupamentos foram bem definidos e posteriormente, validando os agrupamentos.
| Índice de Rand | Índice de Procrustes | Acurácia | |
|---|---|---|---|
| $K$-médias | 0,696 | 0,419 | 82,1% |
Conclusões
Neste trabalho, apresentamos uma introdução a análise estatística de formas e classificação não supervisionada no espaço não euclidiano.
No geral, os resultados obtidos mostraram que o algoritmo proposto obteve bom desempenho, para realizar os agrupamentos, usando dados de tamanho e forma.
Se tratando dos dados simulados e reais, o algoritmo foi eficiente para todos os cenários propostos. Para o cenário em que os os grupos eram mais homogêneos, o algoritmo perdeu um pouco de eficiência, para grupos mais heterogêneos o algoritmo foi mais eficiente.
Assim, este trabalho contribuiu para a literatura teórica dos métodos de agrupamento para dados de análise estatística de tamanho e forma.