Expansões de Edgeworth para a distribuição Lomax

18-03-2020 1260 words 6 minutes

Contents

Esse trabalho foi apresentado na disciplina de teoria assintotica ministrada pelo Prof. Dr. Gauss Moutinho Cordeiro.

O objetivo deste trabalho é usar uma ferramenta matemática conhecida como expansão de Edgeworth em um conjunto de dados gerados a partir da distribuição lomax. Tal expansão permite obter uma função densidade de probabilidade com assimetria e curtose arbitrárias a partir de uma densidade normal.

Expansão de Edgeworth: Distribuição Lomax

As fórmulas a baixo são as expansões de Edgeworth para as funções densidade e de distribuição de uma soma padronizada $S_n^*$, respectivamente.

Função densidade de Edgeworth

$$f_{S_n^*} (y) = \phi (y) \left\lbrace 1+ \frac{\rho_3}{6\sqrt{n}} H_3 (y) + \frac{\rho_4}{24n} H_4 (y) + \frac{\rho_3^2}{72n} H_6 (y)\right\rbrace + O(n^{-3/2})$$

Função de distribuição de Edgeworth

$$ F_{S_n^*} (y) = \Phi(y) - \phi (y) \left\lbrace 1+ \frac{\rho_3}{6\sqrt{n}} H_2 (y) + \frac{\rho_4}{24n} H_3 (y) + \frac{\rho_3^2}{72n} H_5 (y)\right\rbrace + O(n^{-3/2})$$

Função densidade da lomax

A distribuição Lomax, também chamada de distribuição Pareto Tipo II, é uma distribuição de probabilidade de cauda pesada usada em negócios, economia, ciência atuarial, teoria de filas e modelagem de tráfego da Internet. O criador, Lomax (1987), utilizou a distribuição inicialmente em análises de dados de tempo de vida de falhas de negócios.

Uma variável aleatória $X$ segue a distribuição de Lomax com parâmetros $\lambda >0$ e $\alpha >0$ se sua função de probabilidade for dada por

$$f(x;\alpha,\lambda)={\alpha \over \lambda }\left[{1+{x \over \lambda }}\right]^{-(\alpha +1)}$$

A densidade pode ser reescrita de tal forma que mostre mais claramente a relação com a distribuição de Pareto Tipo I. Isso é:

$$f(x;\alpha,\lambda)={\alpha \lambda ^{\alpha }} \over {(x+\lambda )^{\alpha +1}}.$$

Os momentos da distribuição Lomax são obtidos pela Equação (4); É possível ver a demonstração analítica em Gradshteyn and Ryzhik (2007).

$$\mathbf{E}(X^r) = \dfrac{\alpha \lambda^r \Gamma(r+1) \Gamma(\alpha-r)}{\Gamma(\alpha +1)}, \hspace{0.5cm} \alpha>r$$

Logo, dado a Equação (5) a média e a variância de $X$, são, respectivamente, $$\mathbf{E}(x) = \frac{\lambda}{\alpha-1}, \hspace{0.5cm} \alpha>1$$

e $$Var(x) = {\begin{cases}{\dfrac{\lambda^{2}\alpha}{(\alpha -1)^{2}(\alpha -2)}} \hspace{0.5cm} \alpha >2\end{cases}}.$$

O coeficiente de assimetria da distribuição Lomax é dado por $$\rho_3= {\frac {2(1+\alpha )}{\alpha -3}},{\sqrt {\frac {\alpha -2}{\alpha }}}{\text{ para }}\alpha >3,$$

Respeitando a condição de existência, $\alpha>3$, a distribuição Lomax é sempre assimétrica à direita, independentemente dos valores dos parâmetros. O coeficiente de excesso de curtose da distribuição Lomax é $$\rho_4= \frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}\hspace{0.5cm}{\text{ para }}\alpha >4$$

Respeitando a condição de existência, $\alpha>4$ a distribuição Lomax é leptocúrtico, independentemente dos valores dos parâmetros.

Além da função densidade há outras formas de se caracterizar as distribuições de probabilidade. Para tanto, pode-se utilizar a função geratriz de momentos, função de cumulantes ou a função de distribuição; vale notar que nem todas as distribuições de probabilidade possuem função geratriz de momentos. A função geratriz de momentos de $X$ é dada por $$M_X (t) = \alpha (-t \lambda)^\alpha e^{(-t\lambda)} \Gamma(-\alpha, -t \lambda)$$

e a função de cumulantes: $$K_X(t) = \log(M_Y (t))= \log (\alpha ) - \alpha \log(t\lambda) - t \lambda + \log(\Gamma(-\alpha, -t\lambda))$$

Função densidade de Edgeworth aplicada a lomax

$$f_{S_n^*} (y) = \phi (y) \left\lbrace 1+ \frac{\frac {2(1+\alpha )}{\alpha -3},{\sqrt {\frac {\alpha -2}{\alpha }}}}{6\sqrt{n}} H_3 (y) + \frac{\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{24n} H_4 (y) + \frac{\left({\frac {2(1+\alpha )}{\alpha -3}},{\sqrt {\frac {\alpha -2}{\alpha }}}\right)^2} {72n} H_6 (y)\right\rbrace$$

Função distribuição de Edgeworth aplicada a lomax

$$F_{S_n^*} (y) = \Phi (y) \left\lbrace 1+ \frac{\frac {2(1+\alpha )}{\alpha -3},{\sqrt {\frac {\alpha -2}{\alpha }}}}{6\sqrt{n}} H_2 (y) + \frac{\frac {6(\alpha ^{3}+\alpha ^{2}-6\alpha -2)}{\alpha (\alpha -3)(\alpha -4)}}{24n} H_3 (y) + \frac{\left({\frac {2(1+\alpha )}{\alpha -3}},{\sqrt {\frac {\alpha -2}{\alpha }}}\right)^2} {72n} H_5 (y)\right\rbrace$$

Além disso, a lomax tem varias relações com outras distribuições, algumas delas:

Pareto
Pareto generalizada
prime beta
distribuição F
distribuição q-exponencial
distribuição logística
Outras

Simulação

Sejam $X_1,…,X_n$ variáveis aleatórias com distribuição Lomax, com parâmetros $\lambda=5$, $\alpha=5$. As expansões de Edgeworth para a função densidade com tamanhos n=10, n=50, n=100 e n=200, são apresentadas na Figura a seguir.

n=10

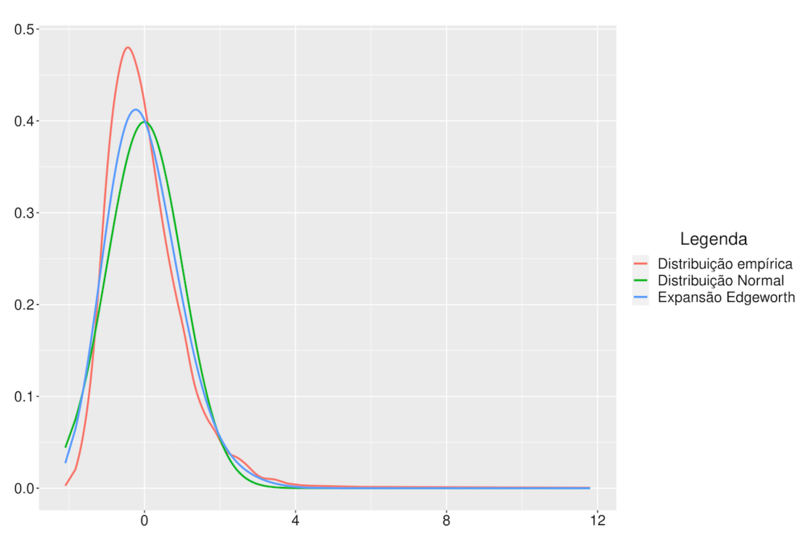
n=50

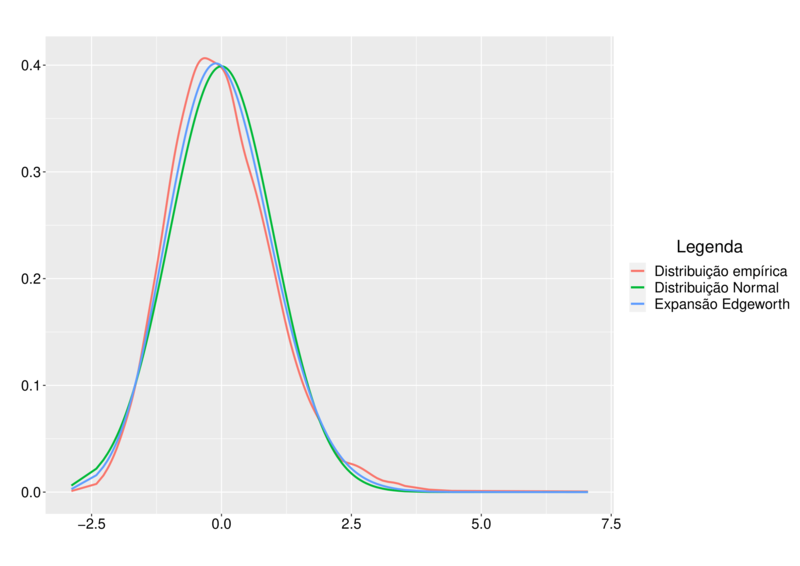
n=100

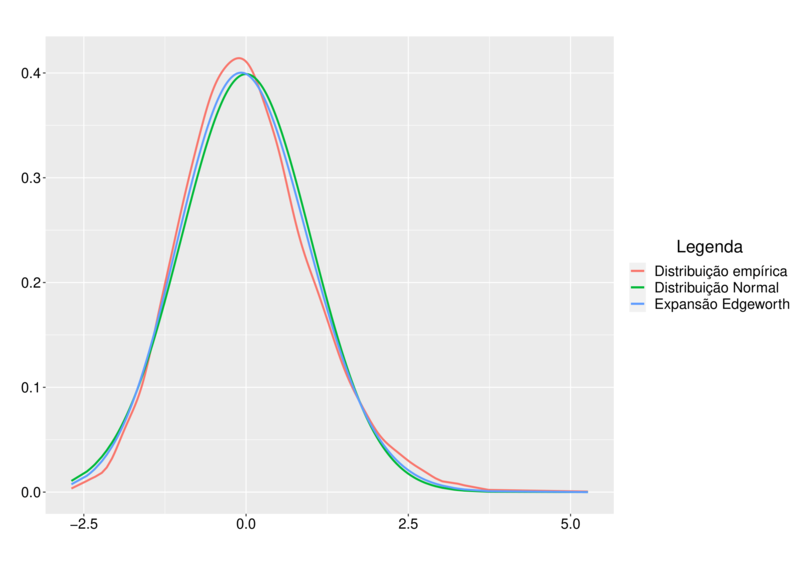
n=200

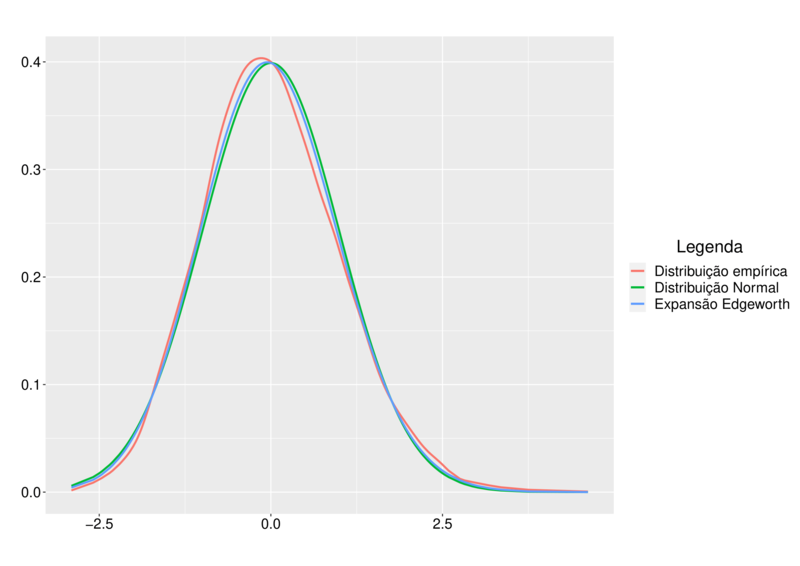
algoritmo para a construção das funções densidade e de distribuição.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


library(EQL)

fp = function(y,n){
  (sqrt(n)*(n+y*sqrt(n))^(n-1)*exp(-n-y*sqrt(n)))/factorial(n-1)
}


edgeworth = function(y, n, rho3, rho4){
  dnorm(y)*(1+(rho3*hermite(y,3)/(6*sqrt(n)))+((rho4*hermite(y,4))/(24*n))
            +((rho3*rho3*hermite(y,6))/(72*n)))
}

Distribuição Lomax

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


library(Renext)
library(ggplot2)

n =100
l = 2
a = 5

mu = l/(a-1)
sigma2 = (a*l^2)/((a-1)^2*(a-2))
rho3 <- log((2*(1+a)*sqrt((a-2)/a))/(a-3))
rho4 <- log((6*(a^3+a^2-6*a-2))/(a*(a-3)*(a-4)))

x = seq(0.0001, 6, 0.1)
y = dlomax(x, scale = l, shape = a)

dados<-data.frame(x,y)

ggplot(dados, aes(x,y)) + geom_line(color=2)

Aproximação Normal pela expansão de Edgeworth para n= 10, 25, 50 e 100.

Para n=10

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


library(EnvStats)
n=10
m = 1000
obs = rlomax(m*n, scale = l, shape = a)

# Distribuição empírica da soma estocástica de Lomax
x = matrix(0, m, n)
for(i in 1:m){
  x[i,] = rlomax(n, scale = l, shape = a)
}

sn = apply(x, 1, sum)

#Trabalhando com a soma estocástica padronizada empírica
snp = (sn-n*mu)/(sqrt(n*sigma2))

x <- qemp(p = seq(0, 1, len = 100), obs = snp)
y <- demp(x, snp)
z <- dnorm(x)
h <- edgeworth(x, n, rho3 = rho3, rho4 = rho4)

dados<-data.frame(x,y,z,h)

ggplot(dados, aes(x,y)) + geom_path(aes(color = 'Distribuição empírica')) + geom_path(aes(x,z, color = 'Normal'))+ geom_path(aes(x,h, color = 'Expansão Edgeworth'))

Para n=25

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


library(EnvStats)
n=25
m = 1000
obs = rlomax(m*n, scale = l, shape = a)

# Distribuição empírica da soma estocástica de Lomax
x = matrix(0, m, n)
for(i in 1:m){
  x[i,] = rlomax(n, scale = l, shape = a)
}

sn = apply(x, 1, sum)

#Trabalhando com a soma estocástica padronizada empírica
snp = (sn-n*mu)/(sqrt(n*sigma2))

x <- qemp(p = seq(0, 1, len = 100), obs = snp)
y <- demp(x, snp)
z <- dnorm(x)
h <- edgeworth(x, n, rho3 = rho3, rho4 = rho4)

dados<-data.frame(x,y,z,h)

ggplot(dados, aes(x,y)) + geom_path(aes(color = 'Distribuição empírica')) + geom_path(aes(x,z, color = 'Normal'))+ geom_path(aes(x,h, color = 'Expansão Edgeworth'))

Para n=50

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


library(EnvStats)
n=50
m = 1000
obs = rlomax(m*n, scale = l, shape = a)

# Distribuição empírica da soma estocástica de Lomax
x = matrix(0, m, n)
for(i in 1:m){
  x[i,] = rlomax(n, scale = l, shape = a)
}

sn = apply(x, 1, sum)

#Trabalhando com a soma estocástica padronizada empírica
snp = (sn-n*mu)/(sqrt(n*sigma2))

x <- qemp(p = seq(0, 1, len = 100), obs = snp)
y <- demp(x, snp)
z <- dnorm(x)
h <- edgeworth(x, n, rho3 = rho3, rho4 = rho4)

dados<-data.frame(x,y,z,h)

ggplot(dados, aes(x,y)) + geom_path(aes(color = 'Distribuição empírica')) + geom_path(aes(x,z, color = 'Normal'))+ geom_path(aes(x,h, color = 'Expansão Edgeworth'))

Para n=100

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


library(EnvStats)
n=100
m = 1000
obs = rlomax(m*n, scale = l, shape = a)

# Distribuição empírica da soma estocástica de Lomax
x = matrix(0, m, n)
for(i in 1:m){
  x[i,] = rlomax(n, scale = l, shape = a)
}

sn = apply(x, 1, sum)

#Trabalhando com a soma estocástica padronizada empírico
snp = (sn-n*mu)/(sqrt(n*sigma2))

x <- qemp(p = seq(0, 1, len = 100), obs = snp)
y <- demp(x, snp)
z <- dnorm(x)
h <- edgeworth(x, n, rho3 = rho3, rho4 = rho4)

dados<-data.frame(x,y,z,h)

ggplot(dados, aes(x,y)) + geom_path(aes(color = 'Distribuição empírica')) + geom_path(aes(x,z, color = 'Normal'))+ geom_path(aes(x,h, color = 'Expansão Edgeworth'))