Resistência dos vidros (voltagem x temperatura)

10-02-2020 1905 words 9 minutes

Contents

Na minha graduação fiz vários relatórios, das mais diversas disciplinas. Aqui, irei apresentar um resumo de um desses relatórios. Esse Relatório foi feito na disciplina de MLG, ministrado pela Prof. Dra. Michelli Karinne Barros da Silva.

Introdução

O objetivo desse trabalho é saber de que forma os níveis de voltagem e temperatura afetam o tempo médio de resistência dos vidros.

Primeiramente foi feito uma análise descritiva dos dados, mostrando a influencia dos dados sobre a variável resposta. E logo após, o ajuste do modelo para mostrar que as variáveis voltagem e temperatura interferem na resistência dos vidros.

Análise de Dados

Nas tabelas abaixo são apresentados os resultados de um experimento, em que a resistência (em horas) de um determinado tipo de vidro, foi avaliada segundo quatro níveis de voltagem (em kilovolts) e duas temperaturas (em graus Celsius).

Dados do Experimento

Voltagens com temperatura de 170c

200kV	250kV	300kV	350kV
439h	572h	315h	258h
904h	690h	315h	258h
1092h	904h	439h	347h
1105h	1090h	628h	588h

Voltagens com temperatura de 180c

200kV	250kV	300kV	350kV
959h	216h	241h	241h
1065h	315h	315h	241h
1065h	455h	332h	435h
1087h	473h	380h	455h

Análise Descritiva

Na tabela abaixo são apresentadas as médias, desvios e coeficiente de variação das variáveis Resistência, voltagem e temperatura. Podemos perceber que a resistência média foi de 569,34 ao passo que a voltagem e a temperatura apresentaram médias iguais a 275 e 175, respectivamente. O coeficiente de variação da resistência é próximo de 56%, indicando assim, uma alta dispersão nos dados.

Algumas estatísticas para cada variável

	Resistência	Voltagem	Temperatura
Média	569,34	275	175
Desvio	316,98	56,80	5,08
CV	55,67%	20,65 %	2.90 %

Nas tabelas abaixo, fixando cada uma das co-variáveis, nota-se valores maiores para a resistência média com a menor temperatura (170c) e menor voltagem (200kV). Todavia, o coeficiente de variação apesar de diminuir quando fixa-se as co-variáveis, apresenta uma dispersão média dos dados.

Resistencia fixando a temperatura

	Resistência à 170c	Resistência à 180c
Média	621,50	517,19
Desvio	309,47	325,67
CV	49,80%	62,97%

Resistencia fixando as voltagens

	Resistência à 200kv	Resistência à 250kv	Resistência à 300kv	Resistência à 350kv
Média	964,50	589,38	370,63	352,88
Desvio	223,94	294,31	118,67	128,47
CV	23,21%	49,93%	32,01%	36,40%

Percebe-se que as maiores médias da resistência, foram com menor voltagem 200kv e temperatura 170c.

É possível ver também esses dois fatores acontecendo no gráfico abaixo. 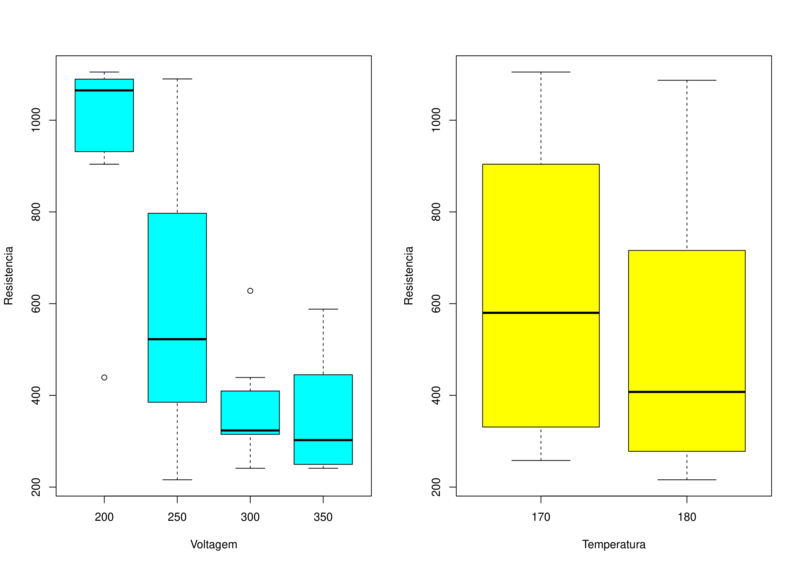Nota-se duas observações discrepantes nos dados, uma com voltagem a 200kV e a outra a 300kV.

Ainda é possível ver a voltagem e temperatura interagindo sobre a resistência do vidro. Como é mostrado no gráfico abaixo

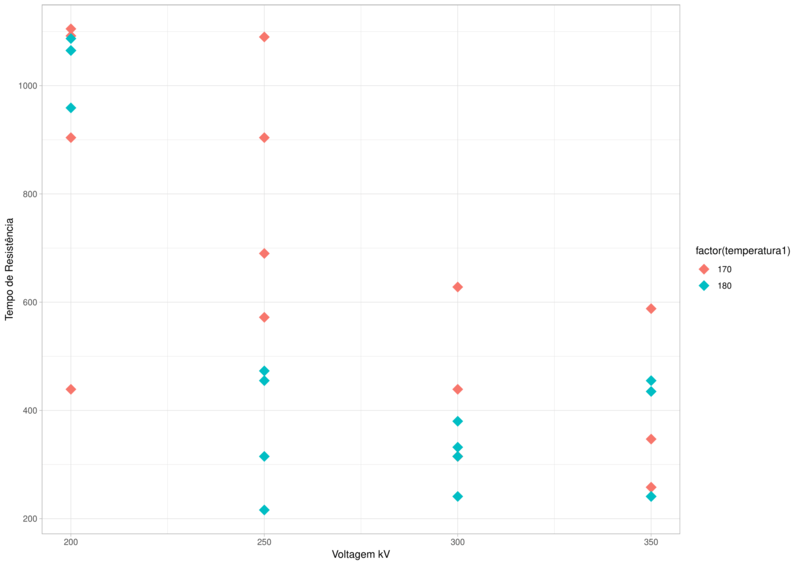
Ainda, podemos fixar as duas variáveis voltagem e temperatura e ver as estatísticas descritivas para cada uma delas.

Algumas estatísticas para a resistência fixando a temperatura a 170c e variando a voltagem

	Resistência à 200kv e 170c	Resistência à 250kv e 170c	Resistência à 300kv e 170c	Resistência à 350kv e 170c
Média	885,00	814,00	424,25	362,75
Desvio	311,20	229,65	158,88	155,92
CV	35,16 %	28,21%	34,85%	42,98 %

Algumas estatísticas para a resistência fixando a temperatura a 180c e variando a voltagem

	Resistência à 200kv e 180c	Resistência à 250kv e 180c	Resistência à 300kv e 180c	Resistência à 350kv e 180c
Média	1,04	364,75	317,00	343,00
Desvio	5,76	121,74	57,66	118,06
CV	5,52%	33,38%	18,19%	34,42%

O mesmo acontece com a análise anterior, a maior média da resistência se da pela temperatura a 170c e voltagem 200kV, sendo ela 885,00.

Já no gráfico de interação, indica-se uma redução da resistência média à medida que aumenta o nível de voltagem. Além disso, há indicação de interação entre voltagem e temperatura.

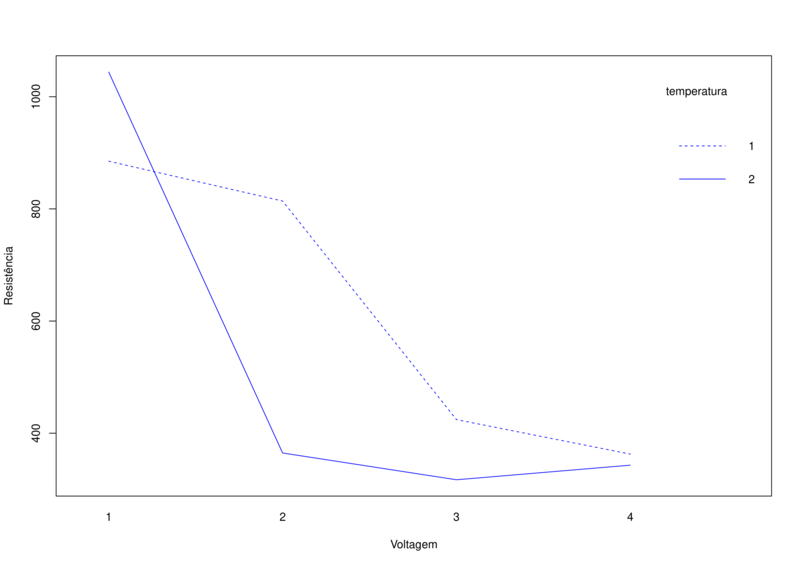
Ajuste do Modelo

Para fazer o ajuste do modelo precisamos saber qual distribuição melhor se encaixa com os dados. Para isso o gráfico abaixo mostra se existe algum tipo de simetria.

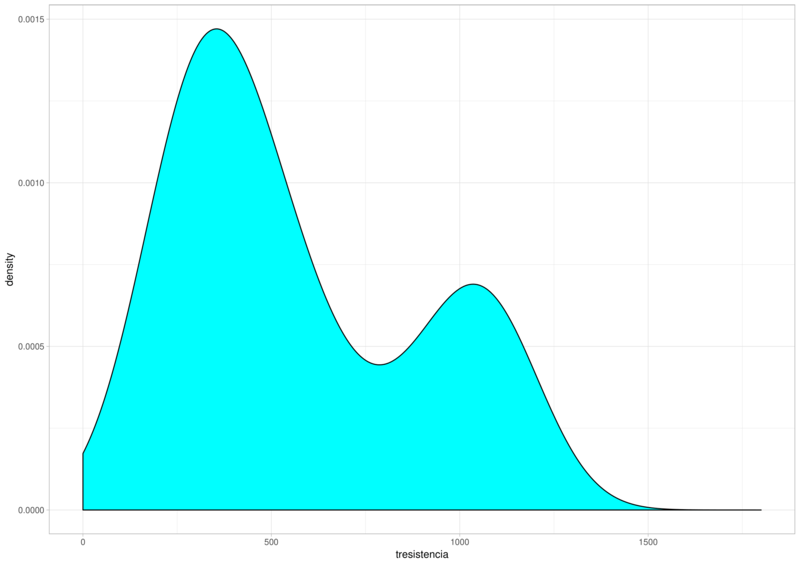
Como o interesse principal desse estudo é comparar as resistências médias, é usual neste tipo de estudo, assumir respostas com alguma distribuição assimétrica. Isso foi comprovado na figura acima, que mostrou possuir assimetria a esquerda. Assim, vamos propor que a variável resposta tenha distribuição gama.

Foram considerado dois ajustes, sem e com interação da voltagem e temperatura.

Na tabela abaixo são apresentados as estimativas do ajuste sem a interação. Todas as estimativas foram bastante significativas.

Variável	Estimativas	P-valor
Intercepto	1039,94	0.00
Voltagem (250kV)	-426,49	0.00
Voltagem (300kV)	-608,81	0.00
Voltagem (350kV)	-612,89	0.00
Temperatura (180c)	-117,78	0.05
phi	9.49 (2,33)	-

No ajuste com interação, algumas variáveis da interação foram significativas a 5%.

Variável	Estimativas	P-valor
Intercepto	885,00	0,00
Voltagem (250kV)	-71,00	0,71
Voltagem (300kV)	-460,75	0,01
Voltagem (350kV)	-522,25	0,00
Temperatura (180c)	159,00	0,46
Voltagem (250kV) : Temperatura (180c)	-608,25	0,03
Voltagem (300kV) : Temperatura (180c)	-266,25	0,26
Voltagem (350kV) : Temperatura (180c)	-178,75	0,44
phi	13,35 (3,30)	-

Para decidir qual ajuste usar, foi feito um teste F utilizando os dois ajustes. As hipóteses do teste F são:

$H_0$: Teste sem interação;

$H_1$: Teste com interação

As estimativas do teste F foram:

Teste F	P-valor
3.45	0.0325

No qual, foi mostrado que o ajuste com interação é mais apropriado ao nível de significância a 5%. Porém a 1% o mesmo deixa de ser significativo, nos mostrando que não a diferença de escolha.

Inicialmente foi feito uma seleção de variáveis através do método AKAIKE. Contudo, nenhuma variável deixou de ser significativa, nos mostrando que a resistência depende da voltagem e temperatura.

Na Figura abaixo são apresentados alguns gráficos de diagnóstico, notamos uma discrepância da observação 16, que aparece como ponto influente e aberrante. Além disso, notamos indícios de heteroscedasticidade, ou seja, uma diminuição da variabilidade com o aumento do valor ajustado. Assim, podemos propor um modelo alternativo, que ajuste melhor a variância que o modelo Gamma.

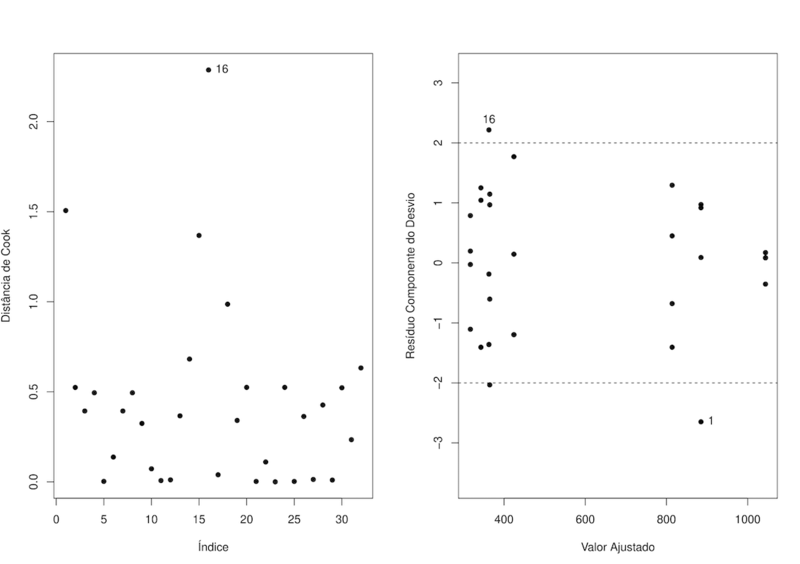
A eliminação desses pontos muda as estimativas, embora não mude a inferência. As novas estimativas são:

	Estimativas sem a obs. 1	Estimativas sem a obs. 16	Estimativas sem as obs. 1 e 16
Intercepto	1033,67	885,00	1033,67
Voltagem (250kV)	-219,67	-71,00	-219,67
Voltagem (300kV)	-609,42	-460,80	-609,42
Voltagem (350kV)	-670,92	-597,30	-746,00
Temperatura (180c)	10,33	159,00	10,33
Voltagem (250kV) e Temperatura (180c)	-459,58	-608,20	-459,58
Voltagem (300kV) e Temperatura (180c)	-117,58	-266,20	-117,58
Voltagem (350kV) e Temperatura (180c)	-30,08	-103,70	45,00
phi	16,00 (4,023)	15,65 (3,93)	19,75 (5,06)

Ao verificar o impacto que houve na retirada dessas obs. Temos :

	Impacto sem a obs. 1	Impacto sem a obs. 16	Impacto sem as obs.1 e 16
Intercepto	-16,80	0,00	-16,80
Voltagem (250kV)	-209,39	0,00	-209,39
Voltagem (300kV)	-32,27	0,00	-32,27
Voltagem (350kV)	-28,47	-14,38	-42,84
Temperatura (180c)	93,50	0,00	93,50
Voltagem (250kV) : Temperatura (180c)	24,44	0,00	24,44
Voltagem (300kV) : Temperatura (180c)	55,84	0,00	55,84
Voltagem (350kV) : Temperatura (180c)	83,17	42,01	125,18

O impacto é bastante alto, dado que o valor esperado para a retirada das duas observações seria de 6,25. Isso acontece pois a adequação do modelo e a existência de observações atípicas estão influenciando diretamente no ajuste. Essa adequação pode ser vista na figura abaixo

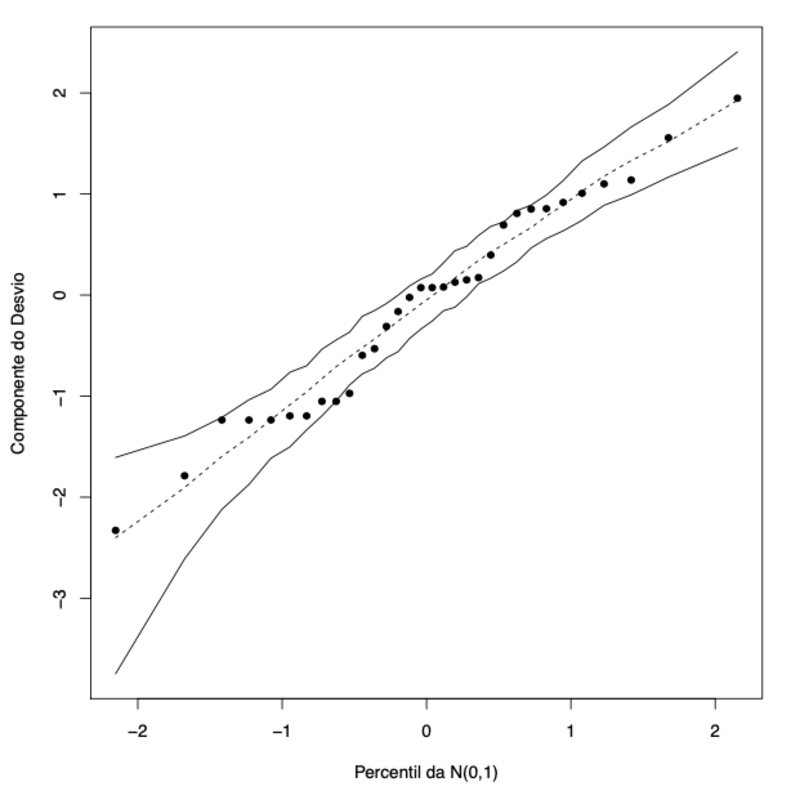
Não observamos pontos muito fora do envelope, porém observamos pontos muito fora do alinhamento. Por conseguinte, há indicação de observações atípicas, e que o modelo seja inadequado.

Conclusão

O que foi visto na análise descritiva se refletiu no ajuste do modelo, as variáveis voltagem e temperatura são extremamente significativas para a resistência do vidro. Mesmo o ajuste Gamma não sendo o melhor.

A voltagem 350kV diminui cerca de 522,25 a resistência do vidro, já a temperatura $180$c aumenta a resistência do vidro em 159,00. Porem, quando fazemos a interação das duas variáveis que é o que realmente interessa, ja que a produção de vidro depende dessas duas variáveis, temos que a voltagem 250kV e a temperatura 180c diminui cerca de 608,25 a resistência do vidro em comparação a voltagem 200kV e a temperatura 170c.

O que podemos afirmar, segundo os dados, que, para se obter uma maior resistência dos vidros, devemos manter em temperatura a 170c e a voltagem 200kV.

R

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182


library(fBasics)
library(ggplot2)
library(MASS)
dados<-read.table('Documentos/UFCG/2018.2/MLG/ANALISES/7/vidros.dat')
names(dados)<-c('tresistencia','voltagem','temperatura')

dados$voltagem1<-1:32
dados$voltagem1[which(dados$voltagem==1)] <-200
dados$voltagem1[which(dados$voltagem==2)] <- 250
dados$voltagem1[which(dados$voltagem==3)] <- 300
dados$voltagem1[which(dados$voltagem==4)] <- 350

dados$temperatura1<-1:32
dados$temperatura1[which(dados$temperatura==1)]<-170
dados$temperatura1[which(dados$temperatura==2)]<-180
dados$temperatura<-factor(dados$temperatura)
dados$voltagem<-factor(dados$voltagem)
attach(dados)

(mgr<-mean(tresistencia))
(mgv<-mean(voltagem1))
(mgt<-mean(temperatura1))

100*(cv1<-sd(tresistencia)/mean(tresistencia))
100*(cv2<-sd(voltagem1)/mean(voltagem1))
100*(cv3<-sd(temperatura1)/mean(temperatura1))


(media_fixo_temperatura170<-sd(split(tresistencia,temperatura1)$'170'))/(media_fixo_temperatura170<-mean(split(tresistencia,temperatura1)$'170'))

(media_fixo_temperatura180<-sd(split(tresistencia,temperatura1)$'180'))/(media_fixo_temperatura180<-mean(split(tresistencia,temperatura1)$'180'))



(media_fixo_voltagem1<-mean(split(tresistencia,voltagem1)$'200'))
(media_fixo_voltagem2<-mean(split(tresistencia,voltagem1)$'250'))
(media_fixo_voltagem3<-mean(split(tresistencia,voltagem1)$'300'))
(media_fixo_voltagem4<-mean(split(tresistencia,voltagem1)$'350'))

sd(split(tresistencia,voltagem1)$'200')/mean(split(tresistencia,voltagem1)$'200')
sd(split(tresistencia,voltagem1)$'250')/mean(split(tresistencia,voltagem1)$'250')
sd(split(tresistencia,voltagem1)$'300')/mean(split(tresistencia,voltagem1)$'300')
sd(split(tresistencia,voltagem1)$'350')/mean(split(tresistencia,voltagem1)$'350')




dados<-as.data.frame(dados)
par(mfrow=c(1,2))
plot(factor(voltagem1),tresistencia, xlab=('Voltagem'),ylab=('Resistencia'), col=5)
plot(factor(temperatura1),tresistencia, xlab=('Temperatura'),ylab=('Resistencia'),col=7)

ggplot(dados,aes(y=tresistencia,x=voltagem1, fill = factor(temperatura1)))+ geom_col() + labs(x = "Voltagem kV",y = "Tempo de Resistência")+ theme_light()
ggplot(dados,aes(y=tresistencia,x=voltagem1, colour = factor(temperatura1)))+ geom_point(size =5, shape =18) + labs(x = "Voltagem kV",y = "Tempo de Resistência")+ theme_light()

ggplot(dados, aes(x=tresistencia)) + geom_density(fill=5) + xlim(0, 1800)+ theme_light()

modelo<-glm(tresistencia~voltagem + temperatura,family = Gamma(link=identity))
summary(modelo)
xtable(summary(modelo))
with(dados, interaction.plot(voltagem, temperatura, tresistencia, xlab = "Voltagem",
                             ylab = "Resistência", col=4))
summary(modelo)
gamma.shape(modelo)
(modelo1<-glm(tresistencia~voltagem + temperatura + voltagem*temperatura, family = Gamma(link=identity)))
summary(modelo1)
gamma.shape(modelo1)

xtable(anova(modelo,modelo1, test = 'F'))

library(MASS)
(modelo2<-stepAIC(modelo1))
summary(modelo2)
gamma.shape(modelo2)
fit.model<-modelo2
X <- model.matrix(fit.model)
n <- nrow(X)
p <- ncol(X)
w <- fit.model$weights
W <- diag(w)
H <- solve(t(X)%*%W%*%X)
H <- sqrt(W)%*%X%*%H%*%t(X)%*%sqrt(W)
h <- diag(H)
library(MASS)
fi <- gamma.shape(fit.model)$alpha
ts <- resid(fit.model,type="pearson")*sqrt(fi/(1-h))
td <- resid(fit.model,type="deviance")*sqrt(fi/(1-h))
di <- (h/(1-h))*(ts^2)
a <- max(td)
b <- min(td)

plot(fitted(fit.model),h,xlab="Valor Ajustado", ylab="Medida h", pch=16,ylim=c(0,0.5))
#identify(fitted(fit.model), h, n=1)
#
par(mfrow=c(1,2))
plot(di,xlab="Índice", ylab="Distância de Cook", pch=16)
identify(di, n=1)
#
plot(fitted(fit.model),td,xlab="Valor Ajustado", ylab="Resíduo Componente do Desvio",
     ylim=c(b-1,a+1),pch=16)
abline(2,0,lty=2)
abline(-2,0,lty=2)
identify(fitted(fit.model),td, n=2)
#
w <- fit.model$weights
eta <- predict(fit.model)
z <- eta + resid(fit.model, type="pearson")/sqrt(w)
plot(predict(fit.model),z,xlab="Preditor Linear",
     ylab="Variável z", pch=16)

#------------------------------------------------------------#


par(mfrow=c(1,1))
X <- model.matrix(fit.model)
n <- nrow(X)
p <- ncol(X)
w <- fit.model$weights
W <- diag(w)
H <- solve(t(X)%*%W%*%X)
H <- sqrt(W)%*%X%*%H%*%t(X)%*%sqrt(W)
h <- diag(H)
ro <- resid(fit.model,type="response")
fi <- (n-p)/sum((ro/(fitted(fit.model)))^ 2)
td <- resid(fit.model,type="deviance")*sqrt(fi/(1-h))
#
e <- matrix(0,n,100)
#
for(i in 1:100){
  resp <- rgamma(n,fi)
  resp <- (fitted(fit.model)/fi)*resp
  fit <- glm(resp ~ X, family=Gamma(link=log))
  w <- fit$weights
  W <- diag(w)
  H <- solve(t(X)%*%W%*%X)
  H <- sqrt(W)%*%X%*%H%*%t(X)%*%sqrt(W)
  h <- diag(H)
  ro <- resid(fit,type="response")
  phi <- (n-p)/sum((ro/(fitted(fit)))^ 2)
  e[,i] <- sort(resid(fit,type="deviance")*sqrt(phi/(1-h)))}
#
e1 <- numeric(n)
e2 <- numeric(n)
#
for(i in 1:n){
  eo <- sort(e[i,])
  e1[i] <- (eo[2]+eo[3])/2
  e2[i] <- (eo[97]+eo[98])/2}
#
med <- apply(e,1,mean)
faixa <- range(td,e1,e2)
par(pty="s")
qqnorm(td, xlab="Percentil da N(0,1)",
       ylab="Componente do Desvio", ylim=faixa, pch=16, main="")
par(new=TRUE)
#
qqnorm(e1,axes=F,xlab="",ylab="",type="l",ylim=faixa,lty=1, main="")
par(new=TRUE)
qqnorm(e2,axes=F,xlab="",ylab="", type="l",ylim=faixa,lty=1, main="")
par(new=TRUE)
qqnorm(med,axes=F,xlab="", ylab="", type="l",ylim=faixa,lty=2, main="")
#------------------------------------------------------------#                      


modelo3<-glm(tresistencia~voltagem + temperatura + voltagem*temperatura, family = Gamma(link=identity), subset = c(-1))
summary(modelo3)
gamma.shape(modelo3)
modelo4<-glm(tresistencia~voltagem + temperatura + voltagem*temperatura, family = Gamma(link=identity), subset = c(-16))
summary(modelo4)
gamma.shape(modelo4)
modelo5<-glm(tresistencia~voltagem + temperatura + voltagem*temperatura, family = Gamma(link=identity), subset = c(-16,-1))
summary(modelo5)
gamma.shape(modelo5)
impacto1 <- 100*(modelo2$coefficients - modelo3$coefficients)/modelo2$coefficients

impacto2 <- 100*(modelo2$coefficients - modelo4$coefficients)/modelo2$coefficients

impacto3 <- 100*(modelo2$coefficients - modelo5$coefficients)/modelo2$coefficients

esperado <-(2/32)*100

round(impacto2,4)